
 如图所示,已知△EAB所在的平面与矩形ABCD所在的平面互相垂直,EA=EB=3,AD=2,∠AEB=60°,则多面体E-ABCD的外接球的表面积为( )
如图所示,已知△EAB所在的平面与矩形ABCD所在的平面互相垂直,EA=EB=3,AD=2,∠AEB=60°,则多面体E-ABCD的外接球的表面积为( )| A. | $\frac{16π}{3}$ | B. | 8π | C. | 16π | D. | 64π |
分析 设球心到平面ABCD的距离为d,利用△EAB所在的平面与矩形ABCD所在的平面互相垂直,EA=EB=3,∠AEB=60°,可得E到平面ABCD的距离为$\frac{3\sqrt{3}}{2}$,从而R2=($\frac{\sqrt{4+9}}{2}$)2+d2=12+($\frac{3\sqrt{3}}{2}$-d)2,求出R2=4,即可求出多面体E-ABCD的外接球的表面积.
解答 解:设球心到平面ABCD的距离为d,则
∵△EAB所在的平面与矩形ABCD所在的平面互相垂直,EA=EB=3,∠AEB=60°,
∴E到平面ABCD的距离为$\frac{3\sqrt{3}}{2}$,
∴R2=($\frac{\sqrt{4+9}}{2}$)2+d2=12+($\frac{3\sqrt{3}}{2}$-d)2,
∴d=$\frac{\sqrt{3}}{2}$,R2=4,
∴多面体E-ABCD的外接球的表面积为4πR2=16π.
故选:C.
点评 本题考查多面体E-ABCD的外接球的表面积,考查学生的计算能力,正确求出多面体E-ABCD的外接球的半径是关键.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 支持 | a= | c= | |
| 不支持 | b= | d= | |
| 合计 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{13}$ | C. | $\sqrt{15}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{9}$π | B. | $\frac{16}{3}$π | C. | $\frac{64}{9}$π | D. | $\frac{64}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
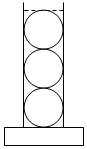 如图,圆柱形容器内盛有高度为6cm的水,若放入3个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球,则球的半径为( )
如图,圆柱形容器内盛有高度为6cm的水,若放入3个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球,则球的半径为( )| A. | 4cm | B. | 3cm | C. | 2cm | D. | 1 cm |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,等腰梯形ABCD中,AB∥CD,DE⊥AB于E,CF⊥AB于F,且AE=BF=EF=2,DE=CF=2.将△AED和△BFC分别沿DE,CF折起,使A,B两点重合,记为点M,得到一个四棱锥M-CDEF,点G,N,H分别是MC,MD,EF的中点.
如图,等腰梯形ABCD中,AB∥CD,DE⊥AB于E,CF⊥AB于F,且AE=BF=EF=2,DE=CF=2.将△AED和△BFC分别沿DE,CF折起,使A,B两点重合,记为点M,得到一个四棱锥M-CDEF,点G,N,H分别是MC,MD,EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 506 | D. | 507 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com