练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．若（2x+$\frac{1}{\sqrt{x}}$）n的展开式中第2项与第3项系数相等，则${∫}_{0}^{3}$xn-2dx=$\frac{81}{4}$．

    分析 由条件可得${C}_{n}^{1}$•2n-1=${C}_{n}^{2}$•2n-2，求得n=5，从而求得${∫}_{0}^{3}$xn-2dx 的值．

    解答 解：∵（2x+$\frac{1}{\sqrt{x}}$）n的展开式中第2项与第3项系数相等，∴${C}_{n}^{1}$•2n-1=${C}_{n}^{2}$•2n-2，求得n=5，
    则${∫}_{0}^{3}$xn-2dx=${∫}_{0}^{3}{x}^{3}dx$=$\frac{{x}^{4}}{4}$${|}_{0}^{3}$=$\frac{81}{4}$，
    故答案为：$\frac{81}{4}$．

    点评 本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．已知函数f（x）是定义在R上的奇函数，且在区间[0，+∞）上是增函数，若$\frac{{|f（lnx）-f（ln\frac{1}{x}）|}}{2}＜f（1）$，则f（x）的取值范围是（　　）
    A．（0，$\frac{1}{e}$）B．（0，e）C．（$\frac{1}{e}$，e）D．（e，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知椭圆C：$\frac{x^2}{4}$+$\frac{y^2}{3}$=1．
    （Ⅰ）求椭圆C的离心率；
    （Ⅱ）若椭圆C与直线y=x+m交于M，N两点，且|MN|=$\frac{{12\sqrt{2}}}{7}$，求m的值；
    （Ⅲ）若点A（x1，y1）与点P（x2，y2）在椭圆C上，且点A在第一象限，点P在第二象限，点B与点A关于原点对称，求证：当x12+x22=4时，三角形△PAB的面积为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

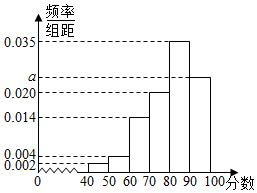    8．2015年，威海智慧公交建设项目已经基本完成．为了解市民对该项目的满意度，分别从不同公交站点随机抽取若干市民对该项目进行评分（满分100分），绘制如下频率分布直方图，并将分数从低到高分为四个等级：
    满意度评分低于60分60分到79分80分到89分不低于90分
    满意度等级不满意基本满意满意非常满意
    已知满意度等级为基本满意的有680人．
    （I）求等级为非常满意的人数：
    （Ⅱ）现从等级为不满意市民中按评分分层抽取6人了解不满意的原因，并从中选取3人担任整改监督员，求3人中恰有1人评分在[40，50）的概率；
    （Ⅲ）相关部门对项目进行验收，验收的硬性指标是：市民对该项目的满意指数不低于0.8，否则该项目需进行整改，根据你所学的统计知识，判断该项目能否通过验收，并说明理由．（注：满意指数=$\frac{满意程度的平均分}{100}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．（$\frac{i-1}{i+1}$）2016的共轭复数为（　　）
    A．-1B．1C．1-iD．-1+i

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．某位同学进行寒假社会实践活动，为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究，他分别记录了1月11日至1月15日的白天平均气温x（℃）与该奶茶店的这种饮料销量y（杯）得到如下数据
    日期11日12日13日14日15日
    平均气温x（℃）91012118
    销量y（杯）2325302621
    （1）若先从这5组数据中抽取2组，列出所有可能的结果并求抽出的2组数据恰好是相邻2天数据的概率；
    （2）请根据所给的5组数据求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$，并根据线性回归方程预测当气象台预报1月16日的白天气温为7℃时奶茶店这种饮料的销量（结果四舍五入）．
    附：线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中$\left\{\begin{array}{l}{\widehat{b}=\underset{\stackrel{n}{∑}}{i=1}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）=\frac{\underset{\stackrel{n}{∑}}{i=1}{x}_{i}{y}_{i}-n\overline{xy}}{\underset{\stackrel{n}{∑}}{i=1}{{x}_{i}}^{2}-n\overline{{x}^{2}}}}\\{\widehat{a}=\overline{y}-\widehat{b}\overline{x}}\end{array}\right.$，其中$\overline{x}$，$\overline{y}$为样本平均值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=sin（2ωx-$\frac{π}{6}}$）-4sin2ωx（ω＞0），其图象相邻的两个对称中心之间的距离为$\frac{π}{2}$．
    （1）求函数f（x）的解析式；
    （2）将函数f（x）的图象向右平移$\frac{π}{3}$个单位，得到函数g（x）的图象，试讨论g（x）在[-$\frac{π}{6}$，$\frac{π}{2}}$]上的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

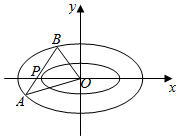    9．设椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1的离心率e=$\frac{1}{2}$，动点P在椭圆C上，点P到椭圆C的两个焦点的距离之和是4．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）若椭圆C1的方程为$\frac{x^2}{m^2}$+$\frac{y^2}{n^2}$=1（m＞n＞0），椭圆C2的方程为$\frac{x^2}{m^2}$+$\frac{y^2}{n^2}$=λ（λ＞0，且λ≠1），则称椭圆C2是椭圆C1的λ倍相似椭圆．已知椭圆C2是椭圆C的3倍相似椭圆．若过椭圆C上动点P的切线l交椭圆C2于A，B两点，O为坐标原点，试证明当切线l变化时|PA|=|PB|并研究△OAB面积的变化情况．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图，茎表示得分的十位数，据图可知甲运动员得分的中位数和乙运动员得分的众数之和为64．

    查看答案和解析>>

    同步练习册答案