在棱长为1的正方体ABCD-A1B1C1D1中.
(1)求:点A到平面BD1的距离;
(2)求点A1到平面AB1D1的距离;
(3)求平面AB1D1与平面BC1D的距离;
(4)求直线AB到CDA1B1的距离.
分析:(1)根据点A在平面BD
1内,即可求出点A到平面BD
1的距离;
(2)根据点A
1到平面AB
1D
1的距离是正方体的体对角线的
,而正方体的体对角线为
,即可求出点A
1到平面AB
1D
1的距离;
(3)根据平面AB
1D
1∥平面BC
1D,可知这两个平面将体对角线分成三等分,从而求出平面AB
1D
1与平面BC
1D的距离;
(4)先求出A到CDA
1B
1的距离,而AB∥平面CDA
1B
1,则直线AB到CDA
1B
1的距离等于点A到CDA
1B
1的距离.
解答:解:
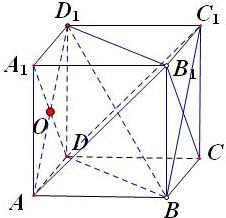
(1)因为点A在平面BD
1内
∴点A到平面BD
1的距离为0
(2)正方体的体对角线为
而点A
1到平面AB
1D
1的距离是正方体的体对角线的
∴点A
1到平面AB
1D
1的距离为
;
(3)平面AB
1D
1∥平面BC
1D
这两个平面将体对角线分成三等分
∴平面AB
1D
1与平面BC
1D的距离为
;
(4)∵AO⊥A
1D
∴A到CDA
1B
1的距离为AO=
而AB∥平面CDA
1B
1∴直线AB到CDA
1B
1的距离
点评:本题主要考查了点到平面的距离,以及直线到平面的距离,同时考查了空间想象能力,计算推理能力,属于基础题.

 (1)因为点A在平面BD1内
(1)因为点A在平面BD1内

 小题狂做系列答案
小题狂做系列答案 在线段AD1上运动,给出以下四个命题:
在线段AD1上运动,给出以下四个命题: (理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F.
(理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F. (2004•武汉模拟)(文科)在棱长为1的正方体ABCD-A′B′C′D′中,AC′为对角线,M、N分别为BB′,B′C′中点,P为线段MN中点.
(2004•武汉模拟)(文科)在棱长为1的正方体ABCD-A′B′C′D′中,AC′为对角线,M、N分别为BB′,B′C′中点,P为线段MN中点.