
【题目】已知圆![]() 恰好经过椭圆
恰好经过椭圆![]() 的两个焦点和两个顶点.
的两个焦点和两个顶点.
(1)求椭圆![]() 的方程;
的方程;
(2)经过原点的直线![]() (不与坐标轴重合)交椭圆
(不与坐标轴重合)交椭圆![]() 于
于![]() 两点,
两点, ![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() 并延长
并延长![]() 交椭圆
交椭圆![]() 于
于![]() ,证明:以线段
,证明:以线段![]() 为直径的圆经过点
为直径的圆经过点![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】试题分析:(1)由![]() 恰好经过椭圆
恰好经过椭圆![]() 的两个焦点和两个顶点可得
的两个焦点和两个顶点可得![]() ,
, ![]() 从而可得椭圆
从而可得椭圆![]() 的方程;(2)设直线
的方程;(2)设直线![]() 的斜率为
的斜率为![]() ,可得线
,可得线![]() 的斜率为
的斜率为![]() ,
, ![]() 的方程为
的方程为![]() ,与椭圆方程联立,利用韦达定理求得
,与椭圆方程联立,利用韦达定理求得![]() 的坐标,可得直线
的坐标,可得直线![]() 的斜率为
的斜率为![]() ,即得
,即得![]() ,以线段
,以线段![]() 为直径的圆一定经过点
为直径的圆一定经过点![]() .
.
试题解析:(1)由题意可知, ![]() ,
, ![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)证明:设直线![]() 的斜率为
的斜率为![]() ,
, ![]() ,在直线
,在直线![]() 的方程为
的方程为![]() ,
,
![]() .
.
直线![]() 的斜率为
的斜率为![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,
,
联立 得
得![]() ,
,
记![]() 横坐标分別为
横坐标分別为![]() .由韦达定理知:
.由韦达定理知: ![]() ,
,
所以![]() ,于是
,于是![]() ,
,
所以直线![]() 的斜率为
的斜率为 ,
,
因为![]() .所以
.所以![]() ,
,
所以以线段![]() 为直径的圆一定经过点
为直径的圆一定经过点![]() .
.
【方法点晴】本题主要考查待定系数法求椭圆标准方程及曲线过定点问题,属于难题.解决曲线过定点问题一般有两种方法:① 探索曲线过定点时,可设出曲线方程 ,然后利用条件建立等量关系进行消元,借助于曲线系的思想找出定点,或者利用方程恒成立列方程组求出定点坐标.② 从特殊情况入手,先探求定点,再证明与变量无关.


科目:高中数学 来源: 题型:
【题目】4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜”

(1)求![]() 的值并估计全校3000名学生中读书谜大概有多少?(将频率视为概率)
的值并估计全校3000名学生中读书谜大概有多少?(将频率视为概率)
(2)根据已知条件完成下面2×2的列联表,并据此判断是否有99%的把握认为“读书谜”与性别有关?
非读书迷 | 读书迷 | 合计 | |
男 | 15 | ||
女 | 45 | ||
合计 |
附:![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
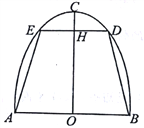
【题目】如图,小明想将短轴长为2,长轴长为4的一个半椭圆形纸片剪成等腰梯形ABDE,且梯形ABDE内接于半椭圆,DE∥AB,AB为短轴,OC为长半轴
(1)求梯形ABDE上底边DE与高OH长的关系式;
(2)若半椭圆上到H的距离最小的点恰好为C点,求底边DE的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]() ,
, ![]() .
.
(1)若![]() ,且直线
,且直线![]() 分别与函数
分别与函数![]() 和
和![]() 的图象交于
的图象交于![]() ,求
,求![]() 两点间的最短距离;
两点间的最短距离;
(2)若![]() 时,函数
时,函数![]() 的图象恒在
的图象恒在![]() 的图象上方,求实数
的图象上方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知与曲线![]() 相切的直线
相切的直线![]() ,与
,与![]() 轴,
轴, ![]() 轴交于
轴交于![]() 两点,
两点, ![]() 为原点,
为原点, ![]() ,
, ![]() ,(
,( ![]() ).
).
(1)求证:: ![]() 与
与![]() 相切的条件是:
相切的条件是: ![]() .
.
(2)求线段![]() 中点的轨迹方程;
中点的轨迹方程;
(3)求三角形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的对称轴为坐标轴,离心率为
的对称轴为坐标轴,离心率为![]() ,且一个焦点坐标为
,且一个焦点坐标为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,以线段
两点,以线段![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,其中点
,其中点![]() 在椭圆
在椭圆![]() 上,
上, ![]() 为坐标原点,求点
为坐标原点,求点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com