
【题目】已知椭圆![]() 的对称轴为坐标轴,离心率为
的对称轴为坐标轴,离心率为![]() ,且一个焦点坐标为
,且一个焦点坐标为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,以线段
两点,以线段![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,其中点
,其中点![]() 在椭圆
在椭圆![]() 上,
上, ![]() 为坐标原点,求点
为坐标原点,求点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:
(1)由题意可求得![]() ,
, ![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.
(2)首先讨论斜率存在的情况,点![]() 到直线
到直线![]() 的距离的最小值为
的距离的最小值为![]() .
.
当斜率不存在时额外讨论可得结论.
试题解析:
解:(1)由已知设椭圆![]() 的方程为
的方程为![]() ,则
,则![]() .
.
由![]() ,得
,得![]() ,
, ![]() ,
, ![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.
(2)当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() 的方程为
的方程为![]() .
.
则由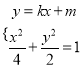 消去
消去![]() 得
得![]() .
.
![]() .①
.①
设点![]() ,
, ![]() ,
, ![]() 的坐标分别是
的坐标分别是![]() ,
, ![]() ,
, ![]() .
.
∵四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
![]() ,
,
由于点![]() 在椭圆
在椭圆![]() 上,∴
上,∴![]() ,
,
从而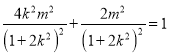 ,化简得
,化简得![]() ,经检验满足①式.
,经检验满足①式.
又点![]() 到直线
到直线![]() 的距离为
的距离为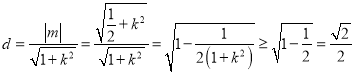 .
.
当且仅当![]() 时,等号成立.
时,等号成立.
当直线![]() 斜率不存在时,由对称性知,点
斜率不存在时,由对称性知,点![]() 一定在
一定在![]() 轴上,
轴上,
从而点![]() 的坐标为
的坐标为![]() 或
或![]() ,直线
,直线![]() 的方程为
的方程为![]() ,∴点
,∴点![]() 到直线
到直线![]() 的距离为1.
的距离为1.
∴点![]() 到直线
到直线![]() 的距离的最小值为
的距离的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知圆![]() 恰好经过椭圆
恰好经过椭圆![]() 的两个焦点和两个顶点.
的两个焦点和两个顶点.
(1)求椭圆![]() 的方程;
的方程;
(2)经过原点的直线![]() (不与坐标轴重合)交椭圆
(不与坐标轴重合)交椭圆![]() 于
于![]() 两点,
两点, ![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() 并延长
并延长![]() 交椭圆
交椭圆![]() 于
于![]() ,证明:以线段
,证明:以线段![]() 为直径的圆经过点
为直径的圆经过点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高二丈,问积几何?”其意思为:“今有底面为矩形的屋脊状的锲体,下底面宽3丈,长4丈,上棱长2丈,高2丈,问:它的体积是多少?”已知1丈为10尺,该锲体的三视图如图所示,则该锲体的体积为( )
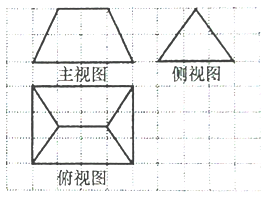
A. 10000立方尺 B. 11000立方尺 C. 12000立方尺 D. 13000立方尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,气象部门预报,在海面上生成了一股较强台风,在据台风中心60千米的圆形区域内将受到严重破坏,台风中心这个从海岸M点登陆,并以72千米/小时的速度沿北偏西60°的方向移动,已知M点位于A城的南偏东15°方向,距A城 ![]() 千米;M点位于B城的正东方向,距B城
千米;M点位于B城的正东方向,距B城 ![]() 千米,假设台风在移动的过程中,其风力和方向保持不变,请回答下列问题:
千米,假设台风在移动的过程中,其风力和方向保持不变,请回答下列问题: 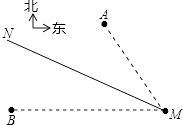
(1)A城和B城是否会受到此次台风的侵袭?并说明理由;
(2)若受到此次台风的侵袭,改城受到台风侵袭的持续时间有多少小时?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com