从边长为2a的正方形纸片的四角各剪去一小块边长为x(0＜x＜a)的正方形后再折成一个无盖的盒子.则x为何值时.盒子容积最大?求容积的最大值. 题目和参考答案——青夏教育精英家教网—

从边长为2a的正方形纸片的四角各剪去一小块边长为x（0＜x＜a)的正方形后再折成一个无盖的盒子，则x为何值时，盒子容积最大?求容积的最大值.

答案：
解析：

解：∵0＜x＜a ∴a－x＞0

依题意，得：Ｖ=x（2a－2x）²

=2·2x·（a－x）（a－x）

≤2·［］³=a³

当且仅当2x=a－x，即x=时，盒子的容积最大，且容积的最大值为a³.

练习册系列答案

金版新学案夏之卷假期作业河北科学技术出版社系列答案

相关习题

科目：高中数学 来源： 题型：

从边长为2a的正方形铁片的四个角各截去一个边为x的正方形，再将四边向上折起，做成一个无盖的长方形铁盒，要求长方体的高度与底面边的比值不超过常数t（t＞0）．试问当x取何值时，容量V有最大值．

科目：高中数学 来源： 题型：

从边长为2a的正方形铁皮的四个角各截去一个边长为x的小正方形，再将四边向上折起，做成一个无盖的长方体铁盒，且要求长方体的高度x与底面正方形的边长的比不超过常数t．问：
（1）求长方体的容积V关于x的函数表达式；
（2）x取何值时，长方体的容积V有最大值？

科目：高中数学 来源：2011——2012学年湖北省洪湖二中高三八月份月考试卷理科数学 题型：解答题

（本题满分12分）
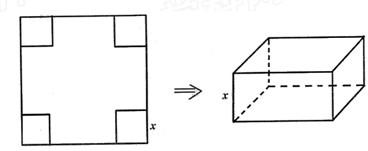
从边长为2a的正方形铁皮的四个角各截去一个边长为x的小正方形，再将四边向上折起，做成一个无盖的长方体铁盒，且要求长方体的高度x与底面正方形的边长的比不超过常数t.
问：（1）求长方体的容积V关于x的函数表达式；（2）x取何值时，长方体的容积V有最大值？

科目：高中数学 来源：2010-2011学年湖北省宜昌市夷陵中学、荆门市钟祥一中高三第二次联考数学试卷（文科）（解析版） 题型：解答题

科目：高中数学 来源：2010-2011学年湖北省、钟祥一中高三第二次联考数学理卷 题型：解答题

（12分）如图，从边长为2a的正方形铁皮的四个角各截去一个边长为x的小正方形，再将四边向上折起，做成一个无盖的长方体铁盒，且要求长方体的高度x与底面正方形的边长的比不超过常数t，问：x取何值时，长方体的容积V有最大值？

同步练习册答案