
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
分析 根据已知条件,作出图形,MN的中点连接椭圆的两个焦点,便会得到三角形的中位线,根据中位线的性质及椭圆上的点到两焦点的距离和为2a即可求出|AN|+|BN|.
解答 解:设MN的中点为Q,椭圆C的左右焦点分别为F1,F2,
如图,连接QF1,QF2,
∵F1是MA的中点,Q是MN的中点,
∴F1Q是△MAN的中位线;
丨QF1丨=$\frac{1}{2}$丨AN丨,
同理:丨QF2丨=$\frac{1}{2}$丨NB丨,
∵Q在椭圆C上,
∴|QF1|+|QF2|=2a=6,
∴|AN|+|BN|=12.
故选D.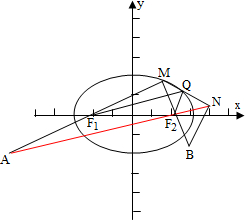
点评 本题考查椭圆的定义,椭圆的基本性质的应用,三角形的中位线定理,属于中档题.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | 12 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAD=90°,A1C1⊥B1D,BC=1,AD=AA1=3.
如图,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAD=90°,A1C1⊥B1D,BC=1,AD=AA1=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
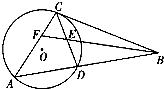 如图,D是△ABC边AB上的一点,△ACD内接于圆O,且∠CAD=∠BCD,E是CD的中点,BE的延长线交AC于点F,证明:
如图,D是△ABC边AB上的一点,△ACD内接于圆O,且∠CAD=∠BCD,E是CD的中点,BE的延长线交AC于点F,证明:查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | ①②③ | B. | ②③ | C. | ①②④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 70 m | B. | 72 m | C. | 75 m | D. | 80 m |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | c<a<b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com