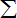“―÷Σ ΐΝ–{a
n}ΒΡ«ΑnœνΚΆ
Sn=2+(n-1)()n-1(nΓ N*)Θ§‘ρ¥φ‘Ύ ΐΝ–{x
n}Θ§{y
n}Θ§ ΙΒΟΘΚΘ®ΓΓΓΓΘ©
| AΘ°an=xn+ynΘ§nΓ N*Θ§Τδ÷–{xn}Θ§{yn}ΈΣΒ»≤ν ΐΝ– |
| BΘ°an=xnynΘ§nΓ N*Θ§Τδ÷–{xn}Θ§{yn}ΈΣΒ»±» ΐΝ– |
| CΘ°an=xn+ynΘ§nΓ N*Θ§Τδ÷–{xn}ΈΣΒ»≤ν ΐΝ–Θ§{yn}ΈΣΒ»±» ΐΝ– |
| DΘ°an=xnynΘ§nΓ N*Θ§Τδ÷–{xn}ΈΣΒ»≤ν ΐΝ–Θ§{yn}ΈΣΒ»±» ΐΝ– |
Β±n=1 ±Θ§a
1=S
1=aȧ
Β±nΓί2 ±Θ§a
n=S
n-S
n-1=[
2+(n-1)()n-1]-[
2+(n-2)()n-2]
=
(n-1)()n-1-
(n-2)()n-2=
(n-1)()n-1-
(2n-4)()n-1=
(3-n)()n-1Ννx
n=3-nȧy
n=
()n-1‘ρ{x
n}ΈΣΒ»≤ν ΐΝ–Θ§{y
n}ΈΣΒ»±» ΐΝ–
Ι a
n=x
ny
nȧnà N
*Θ§Τδ÷–{x
n}ΈΣΒ»≤ν ΐΝ–Θ§{y
n}ΈΣΒ»±» ΐΝ–
Ι ―ΓD
ΝΖœΑ≤αœΒΝ–¥πΑΗ
œύΙΊœΑΧβ
ΩΤΡΩΘΚΗΏ÷– ΐ―ß
ά¥‘¥ΘΚ≤Μœξ
Χβ–ΆΘΚΒΞ―ΓΧβ
‘ΎΒ»±» ΐΝ–{a
n}÷–Θ§»τa
3ΓΔa
7 «ΖΫ≥Χ3x
2-11x+9=0ΒΡΝΫΗυΘ§‘ρa
5ΒΡ÷ΒΈΣΘ®ΓΓΓΓΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß
ά¥‘¥ΘΚ≤Μœξ
Χβ–ΆΘΚΒΞ―ΓΧβ
‘ΎΓςABC÷–Θ§aΘ§bΘ§cΖ÷±π «AΘ§BΘ§CΒΡΕ‘±ΏΘ§“―÷ΣaΘ§bΘ§c≥…Β»±» ΐΝ–Θ§«“a
2-c
2=ac-bcΘ§‘ρ
ΒΡ÷ΒΈΣΘ®ΓΓΓΓΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß
ά¥‘¥ΘΚ≤Μœξ
Χβ–ΆΘΚΫβ¥πΧβ
ΐΝ–{a
n}÷–Θ§a
1=1Θ§
an+1=-an+cΘ®cΘΨ1ΈΣ≥Θ ΐΘ§n=1Θ§2Θ§3Θ§Γ≠Θ©Θ§«“
a3-a2=.Θ®ΔώΘ©«σcΒΡ÷ΒΘΜ
Θ®ΔρΘ©ΔΌ÷ΛΟςΘΚa
nΘΦa
n+1ΘΜ
ΔΎ≤¬≤β ΐΝ–{a
n} «Ζώ”–ΦΪœόΘΩ»γΙϊ”–Θ§–¥≥ωΦΪœόΒΡ÷ΒΘ®≤Μ±Ί÷ΛΟςΘ©ΘΜ
Θ®ΔσΘ©±»Ϋœ
| n |
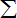 |
| k=1 |
”κ
an+1ΒΡ¥σ–ΓΘ§≤ΔΦ”“‘÷ΛΟςΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß
ά¥‘¥ΘΚ≤Μœξ
Χβ–ΆΘΚΒΞ―ΓΧβ
»τ ΐΝ–{a
n} «Β»±» ΐΝ–Θ§‘ρœ¬Ν– ΐΝ–“ΜΕ® «Β»±» ΐΝ–ΒΡ «Θ®ΓΓΓΓΘ©
| AΘ°{lg} | BΘ°{2+an} | CΘ°{} | DΘ°{} |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß
ά¥‘¥ΘΚ≤Μœξ
Χβ–ΆΘΚΒΞ―ΓΧβ
“―÷ΣΒ»±» ΐΝ–{a
n}ΒΡΙΪ±»ΈΣ
-Θ§‘ρ
| a1+a3+a5+Γ≠+a2n-1 |
| a3+a5+a7+Γ≠+a2n+1 |
=Θ®ΓΓΓΓΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß
ά¥‘¥ΘΚ≤Μœξ
Χβ–ΆΘΚΧνΩ’Χβ
»ΐΗω≤ΜΆ§ΒΡ Β ΐaΘ§bΘ§c≥…Β»≤ν ΐΝ–Θ§«“aΘ§cΘ§b≥…Β»±» ΐΝ–Θ§‘ρaΘΚbΘΚc=______Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß
ά¥‘¥ΘΚ≤Μœξ
Χβ–ΆΘΚΒΞ―ΓΧβ
“―÷ΣΒ»±» ΐΝ–{a
n}¬ζΉψa
1+a
2=4Θ§a
2+a
3=12Θ§‘ρa
5=Θ®ΓΓΓΓΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß
ά¥‘¥ΘΚ≤Μœξ
Χβ–ΆΘΚΫβ¥πΧβ
“―÷Σ ΐΝ–{an}ΈΣΒ»±» ΐΝ–Θ§«“a2=6Θ§6a1+a3=30Θ°
Θ®ΔώΘ©«σanΘ°
Θ®ΔρΘ©…ηbn=log3a1+log3a2+Γ≠+log3anΘ§»τΒ»±» ΐΝ–{an}ΒΡΙΪ±»qΘΨ2Θ§«σ ΐΝ–{bn}ΒΡΆ®œνΙΪ ΫΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>