
【题目】设数列{an}的前n项和为Sn , n∈N* , 已知a1=1,a2= ![]() ,a3=
,a3= ![]() ,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn﹣1 .
,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn﹣1 .
(1)求a4的值.
(2)证明:{an﹣1﹣ ![]() an}为等比数列;
an}为等比数列;
(3)求数列{an}的通项公式.
【答案】
(1)解:∵a1=1,a2= ![]() ,a3=
,a3= ![]() ,
,
∴S1=1,S2= ![]() ,S3=
,S3= ![]() ,
,
又∵4S4+5S2=8S3+S1,
∴S4= ![]() (8S3+S1﹣5S2)=
(8S3+S1﹣5S2)= ![]() (8
(8 ![]() +1﹣5
+1﹣5 ![]() )=
)= ![]() ,
,
∴a4=S4﹣S3= ![]() ﹣
﹣ ![]() =
= ![]()
(2)证明:∵4Sn+2+5Sn=8Sn+1+Sn﹣1,
∴4Sn+2﹣4Sn+1+Sn﹣Sn﹣1=4Sn+1﹣4Sn,
∴4an+2+an=4an+1,
整理得:an﹣2an+1=2an+1﹣4an+2,
∴an+1﹣2an+2= ![]() (an﹣2an+1),
(an﹣2an+1),
即an+2﹣ ![]() an+1=
an+1= ![]() (an+1﹣
(an+1﹣ ![]() an),
an),
又∵ ![]() =
= ![]() ﹣
﹣ ![]() =1,
=1,
∴数列{an+1﹣ ![]() an}是以1为首项、
an}是以1为首项、 ![]() 为公比的等比数列
为公比的等比数列
(3)解:由(2)可知an+1﹣ ![]() an=
an= ![]() ,
,
∴an+1= ![]() an+
an+ ![]() ,
,
∴2n+1an+1=2nan+4,
又∵2a1=2,
∴数列{2nan}是以2为首项、4为公差的等差数列,
∴2nan=2+4(n﹣1)=4n﹣2,
∴an= ![]() =
= ![]()
【解析】(1)通过4S4+5S2=8S3+S1 , 直接代入计算即可;(2)通过对4Sn+2+5Sn=8Sn+1+Sn﹣1变形可知4Sn+2﹣4Sn+1+Sn﹣Sn﹣1=4Sn+1﹣4Sn , 即4an+2+an=4an+1 , 整理得an+1﹣2an+2= ![]() (an﹣2an+1),进而计算可得结论;(3)通过(2)可知an+1﹣
(an﹣2an+1),进而计算可得结论;(3)通过(2)可知an+1﹣ ![]() an=
an= ![]() ,两边同时乘以2n+1可知2n+1an+1=2nan+4,进而数列{2nan}是以2为首项、4为公差的等差数列,计算即得结论.
,两边同时乘以2n+1可知2n+1an+1=2nan+4,进而数列{2nan}是以2为首项、4为公差的等差数列,计算即得结论.
【考点精析】根据题目的已知条件,利用等比关系的确定和数列的通项公式的相关知识可以得到问题的答案,需要掌握等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1﹣ ![]() (x>0),若存在实数a,b(a<b),使y=f(x)的定义域为(a,b)时,值域为(ma,mb),则实数m的取值范围是( )
(x>0),若存在实数a,b(a<b),使y=f(x)的定义域为(a,b)时,值域为(ma,mb),则实数m的取值范围是( )
A.![]()
B.![]()
C.![]() 且m≠0
且m≠0
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=16及圆内一点F(﹣3,0),过F任作一条弦AB. 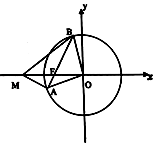
(1)求△AOB面积的最大值及取得最大值时直线AB的方程;
(2)若点M在x轴上,且使得MF为△AMB的一条内角平方线,求点M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin2x的图象向右平移φ(0<φ< ![]() )个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2 , 有|x1﹣x2|min=
)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2 , 有|x1﹣x2|min= ![]() ,则φ=( )
,则φ=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮10% |
| 上两个年度未发生责任道路交通事故 | 下浮20% |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机购为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
(1)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的频率;
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事用户车盈利10000元,且各种投保类型车的频率与上述机构调查的频率一致,完成下列问题:
①若该销售商店内有六辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选两辆车,求这两辆车恰好有一辆为事故车的概率;
②若该销售商一次购进120辆(车龄已满三年)该品牌二手车,求一辆车盈利的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xm﹣ ![]() ,且f(3)=
,且f(3)= ![]() .
.
(1)求函数f(x)的解析式,并判断函数f(x)的奇偶性.
(2)证明函数f(x)在(0,+∞)上的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前我国城市的空气污染越来越严重,空气质量指数![]() 一直居高不下,对人体的呼吸系统造成了严重的影响,现调查了某城市500名居民的工作场所和呼吸系统健康,得到
一直居高不下,对人体的呼吸系统造成了严重的影响,现调查了某城市500名居民的工作场所和呼吸系统健康,得到![]() 列联表如下:
列联表如下:
室外工作 | 室内工作 | 合计 | |
有呼吸系统疾病 | 150 | ||
无呼吸系统疾病 | 100 | ||
合计 | 200 |
(Ⅰ)请把![]() 列联表补充完整;
列联表补充完整;
(Ⅱ)你是否有95%的把握认为感染呼吸系统疾病与工作场所有关;
(Ⅲ)现采用分层抽样从室内工作的居民中抽取一个容量为6的样本,将该样本看成一个总体,从中随机抽取2人,求2人都有呼吸系统疾病的概率.
参考公式与临界表:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com