
【题目】将函数f(x)=sin2x的图象向右平移φ(0<φ< ![]() )个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2 , 有|x1﹣x2|min=
)个单位后得到函数g(x)的图象.若对满足|f(x1)﹣g(x2)|=2的x1、x2 , 有|x1﹣x2|min= ![]() ,则φ=( )
,则φ=( )
A.![]()
B.![]()
C.![]()
D.![]()
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣4x+3,若f(x)≥mx对任意的实数x≥2都成立,则实数m的取值范围是( )
A.[﹣2 ![]() ﹣4,﹣2
﹣4,﹣2 ![]() ?+4]
?+4]
B.(﹣∞,﹣2 ![]() ﹣4]∪[﹣2
﹣4]∪[﹣2 ![]() ?+4,+∞)
?+4,+∞)
C.[﹣2 ![]() ?+4,+∞)
?+4,+∞)
D.(﹣∞,﹣ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,则直线D1E与A1D所成角的大小是 , 若D1E⊥EC,则直线A1D与平面D1DE所成的角为 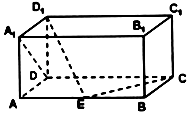
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(ax﹣1)(x﹣1).
(1)若不等式f(x)<0的解集为{x|1<x<2},求实数a的值;
(2)当a>0时,解关于x的不等式f(x)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , n∈N* , 已知a1=1,a2= ![]() ,a3=
,a3= ![]() ,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn﹣1 .
,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn﹣1 .
(1)求a4的值.
(2)证明:{an﹣1﹣ ![]() an}为等比数列;
an}为等比数列;
(3)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在区间D上的函数y=f(x)满足:对x∈D,M∈R,使得|f(x)|≤M恒成立,则称函数y=f(x)在区间D上有界.则下列函数中有界的是: .
①y=sinx;② ![]() ;③y=tanx;④
;③y=tanx;④ ![]() ;
;
⑤y=x3+ax2+bx+1(﹣4≤x≤4),其中a,b∈R.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 为参数),
为参数), ![]() 是
是![]() 上的动点,且满足
上的动点,且满足![]() 为坐标原点),以原点
为坐标原点),以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立坐标系,点
轴的正半轴为极轴建立坐标系,点![]() 的极坐标为
的极坐标为![]() .
.
(1)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的普通方程;
的普通方程;
(2)利用椭圆![]() 的极坐标方程证明
的极坐标方程证明![]() 为定值,并求面积的最大值.
为定值,并求面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com