
分析 (1)问题转化为求函数φ(x)=lnx-x+1零点的个数,求出函数的导数,根据函数的单调性求出函数的零点即可;
(2)求出g(x)的解析式,通过作差法判断即可.
解答 解:(1)曲线y=f(x)与曲线y=x-1公共点的个数等于函数φ(x)=lnx-x+1零点的个数,
∵φ(1)=ln1-1+1=0,故φ(x)存在零点x=1,
又φ′(x)=$\frac{1}{x}$-1=$\frac{1-x}{x}$,(x>0),可得:
0<x<1时,φ′(x)>0,φ(x)递增,
x>1时,φ′(x)<0,φ(x)递减,
故x=1时,φ(x)有极大值也是最大值为φ(1)=0,
即φ(x)≤0恒成立,
故φ(x)存在唯一零点x=1,
∴曲线y=f(x)与曲线y=x-1有唯一公共点(1,0);
(2)由题意得g(x)=ex,
$\frac{g(n)-g(m)}{n-m}$-g($\frac{m+n}{2}$)=$\frac{{e}^{n}{-e}^{m}}{n-m}$-${e}^{\frac{m+n}{2}}$=$\frac{{e}^{\frac{m+n}{2}}}{n-m}$[${e}^{\frac{n-m}{2}}$-${e}^{\frac{m-n}{2}}$-(n-m)]
设函数v(x)=ex-$\frac{1}{{e}^{x}}$-2x,(x≥0),
v′(x)=ex+$\frac{1}{{e}^{x}}$-2≥2$\sqrt{{e}^{x}•\frac{1}{{e}^{x}}}$-2=0,
故v′(x)≥0(仅当x=0时“=”成立),因此v(x)递增,
x>0时,v(x)>v(0)=0,
另x=$\frac{n-m}{2}$,
可得${e}^{\frac{n-m}{2}}$-${e}^{\frac{m-n}{2}}$-(n-m)>0,
故$\frac{g(n)-g(m)}{n-m}$>$g({\frac{m+n}{2}})$.
点评 本题考查了函数的零点问题,考查函数的单调性问题以及代数式的大小比较,是一道中档题.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 明天本地有80%的时间下雨,20%的时间不下雨 | |
| B. | 明天本地有80%的区域下雨,20%的区域不下雨 | |
| C. | 明天本地下雨的机会是80% | |
| D. | 气象局并没有对明天是否下雨作出有意义的预报 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
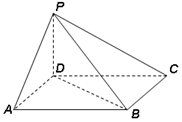 如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2PD=2,PD⊥面ABCD.
如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2PD=2,PD⊥面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{99}$ | B. | $\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{99}$ | C. | 1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{101}$ | D. | $\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{101}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com