
分析 由0<β<α<$\frac{π}{4}$,可得0<α-β<$\frac{π}{4}$,0<α+β<$\frac{π}{2}$,利用已知及同角三角函数基本关系式可求sin(α-β),cos(α+β)的值,根据sin2α=sin[(α-β)+(α+β)]由两角和的正弦函数公式即可求值.
解答 解:∵0<β<α<$\frac{π}{4}$,cos(α-β)=$\frac{12}{13}$,sin(α+β)=$\frac{4}{5}$,
∴0<α-β<$\frac{π}{4}$,0<α+β<$\frac{π}{2}$,
∴sin(α-β)=$\sqrt{1-co{s}^{2}(α-β)}$=$\frac{5}{13}$,cos(α+β)=$\sqrt{1-si{n}^{2}(α+β)}$=$\frac{3}{5}$,
∴sin2α=sin[(α-β)+(α+β)]
=sin(α-β)cos(α+β)+cos(α-β)sin(α+β)
=$\frac{5}{13}$×$\frac{3}{5}$+$\frac{12}{13}$×$\frac{4}{5}$
=$\frac{63}{65}$.
故答案为:$\frac{63}{65}$.
点评 本题主要考查了同角三角函数基本关系式,两角和的正弦函数公式的应用,考查了计算能力和转化思想,属于基本知识的考查.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对任意的x∈R,log2x<0 | B. | 对任意的x∈R,log2x≥0 | ||
| C. | 不存在x∈R,log2x≥0 | D. | 存在x0∈R,log2x0≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
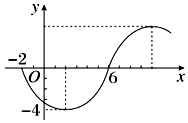
| A. | y=-4sin($\frac{π}{8}$x+$\frac{π}{4}$) | B. | y=4sin($\frac{π}{8}$x-$\frac{π}{4}$) | C. | y=-4sin($\frac{π}{8}$x-$\frac{π}{4}$) | D. | y=4sin($\frac{π}{8}$x+$\frac{π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 交强险浮动因素和浮动费率比率表 | ||
| 浮动因素 | 浮动比率 | |
| A1 | 上一个年度未发生有责任道路交通事故 | 下浮10% |
| A2 | 上两个年度未发生有责任道路交通事故 | 下浮20% |
| A3 | 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| A4 | 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| A5 | 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| A6 | 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
| 类型 | A1 | A2 | A3 | A4 | A5 | A6 |
| 数量 | 10 | 5 | 5 | 20 | 15 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [25,35) | [35,45) | [4,55) | [55,65) | [65,75) | [75,85) | [85,95) |
| 甲厂频数 | 10 | 40 | 115 | 165 | 120 | 45 | 5 |
| 乙厂频数 | 5 | 60 | 110 | 160 | 90 | 70 | 5 |
| P(k2≥k) | 0.05 | 0.01 | 0.001 |
| h | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
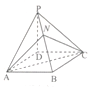 如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与三棱锥D-PAC的体积之比为( )
如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与三棱锥D-PAC的体积之比为( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com