
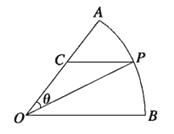
【题目】如图所示,扇形![]() ,圆心角
,圆心角![]() 的大小等于
的大小等于![]() ,半径为2,在半径
,半径为2,在半径![]() 上有一动点
上有一动点![]() ,过点
,过点![]() 作平行于
作平行于![]() 的直线交弧
的直线交弧![]() 于点
于点![]() .
.
(1)若![]() 是半径
是半径![]() 的中点,求线段
的中点,求线段![]() 的大小;
的大小;
(2)设![]() ,求
,求![]() 面积的最大值及此时
面积的最大值及此时![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,定直线
,定直线![]() :
: ![]() ,动圆
,动圆![]() 过点
过点![]() ,且与直线
,且与直线![]() 相切.
相切.
(Ⅰ)求动圆![]() 的圆心轨迹
的圆心轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线与曲线
的直线与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,分别过点
两点,分别过点![]() ,
, ![]() 作曲线
作曲线![]() 的切线
的切线![]() ,
, ![]() ,两条切线相交于点
,两条切线相交于点![]() ,求
,求![]() 外接圆面积的最小值.
外接圆面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:如图,两同心圆: ![]() 和
和![]() .
. ![]() 为大圆上一动点,连结
为大圆上一动点,连结![]() (
(![]() 为坐标原点)交小圆于点
为坐标原点)交小圆于点![]() ,过点
,过点![]() 作
作![]() 轴垂线
轴垂线![]() (垂足为
(垂足为![]() ),再过点
),再过点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() .
.

(1)当点![]() 在大圆上运动时,求垂足
在大圆上运动时,求垂足![]() 的轨迹方程;
的轨迹方程;
(2)过点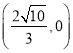 的直线
的直线![]() 交垂足
交垂足![]() 的轨迹于
的轨迹于![]() 两点,若以
两点,若以![]() 为直径的圆与
为直径的圆与![]() 轴相切,求直线
轴相切,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的一块长方体木料中,已知AB=BC=4,AA1=1,设E为底面ABCD的中心,且 ![]() (0≤λ≤
(0≤λ≤ ![]() ),则该长方体中经过点A1、E、F的截面面积的最小值为
),则该长方体中经过点A1、E、F的截面面积的最小值为 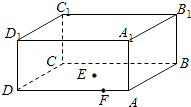
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市某矿山企业生产某产品的年固定成本为![]() 万元,每生产千件该产品需另投入
万元,每生产千件该产品需另投入![]() 万元,设该企业年内共生产此种产品
万元,设该企业年内共生产此种产品![]() 千件,并且全部销售完,每千件的销售收入为
千件,并且全部销售完,每千件的销售收入为![]() 万元,且
万元,且
(Ⅰ)写出年利润![]() (万元)关于产品年产量
(万元)关于产品年产量![]() (千件)的函数关系式;
(千件)的函数关系式;
(Ⅱ)问:年产量![]() 为多少千件时,该企业生产此产品所获年利润最大?
为多少千件时,该企业生产此产品所获年利润最大?
注:年利润=年销售收入-年总成本.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com