
【题目】定义在R上的偶函数f(x)的图象关于点(1,0)对称,且当x∈[1,2]时,f(x)=﹣2x+2,若函数y=f(x)﹣loga(|x|+1)恰好有8个零点,则实数a的取值范围是 .
【答案】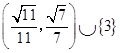
【解析】解:①画出:x∈[1,2]时,f(x)=﹣2x+2,f(x)的图象,
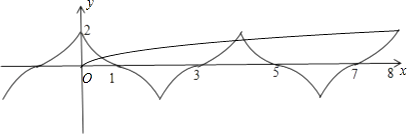
由于函数f(x)的图象关于点(1,0)对称,可得其在区间[0,1]上的图象.
由于函数f(x)是偶函数,且关于点(1,0)对称,则f(﹣x)=f(x),f(x)+f(2﹣x)=0,
可得f(x+4)=f(x),因此其周期T=4.
当a>1时,画出函数y=loga(|x|+1),由于此函数是偶函数,因此只要画出右边的图象即可得出.
由于右边的图象与函数f(x)的图象只有4个交点,因此loga(|8|+1)=2,解得a=3.②当1>a>0时,画出函数y=loga(|x|+1),由于此函数是偶函数,因此只要画出右边的图象即可得出.
由于右边的图象与函数f(x)的图象只有4个交点,因此满足:loga(6+1)>﹣2,loga(10+1)<﹣2,
解得: ![]() <a<
<a< ![]() .
.
故所求的实数a的取值范围是 ![]() .
.
所以答案是: ![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知:θ为第一象限角, ![]() =(sin(θ﹣π),1),
=(sin(θ﹣π),1), ![]() =(sin(
=(sin( ![]() ﹣θ),﹣
﹣θ),﹣ ![]() ),
),
(1)若 ![]() ∥
∥ ![]() ,求
,求 ![]() 的值;
的值;
(2)若| ![]() +
+ ![]() |=1,求sinθ+cosθ的值.
|=1,求sinθ+cosθ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线l的方程为(a+1)x+y+2﹣a=0(a∈R).
(1)若直线l在两坐标轴上的截距相等,求直线l的方程;
(2)若直线l不经过第二象限,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(m,﹣1),
=(m,﹣1), ![]() =(
=( ![]() )
)
(1)若m=﹣ ![]() ,求
,求 ![]() 与
与 ![]() 的夹角θ;
的夹角θ;
(2)设 ![]() . ①求实数m的值;
. ①求实数m的值;
②若存在非零实数k,t,使得[ ![]() +(t2﹣3)
+(t2﹣3) ![]() ]⊥(﹣k
]⊥(﹣k ![]() +t
+t ![]() ),求
),求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点O为圆心的两个同心圆弧和延长后通过点AD的两条线段围成.设圆弧 ![]() 、
、 ![]() 所在圆的半径分别为f(x)、R米,圆心角为θ(弧度).
所在圆的半径分别为f(x)、R米,圆心角为θ(弧度). 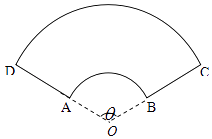
(1)若θ= ![]() ,r1=3,r2=6,求花坛的面积;
,r1=3,r2=6,求花坛的面积;
(2)设计时需要考虑花坛边缘(实线部分)的装饰问题,已知直线部分的装饰费用为60元/米,弧线部分的装饰费用为90元/米,预算费用总计1200元,问线段AD的长度为多少时,花坛的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|f(x)=lg(x﹣1)+ ![]() },集合B={y|y=2x+a,x≤0}.
},集合B={y|y=2x+a,x≤0}.
(1)若a= ![]() ,求A∪B;
,求A∪B;
(2)若A∩B=,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:点M(1,3)不在圆(x+m)2+(y﹣m)2=16的内部,命题q:“曲线 ![]() 表示焦点在x轴上的椭圆”,命题s:“曲线
表示焦点在x轴上的椭圆”,命题s:“曲线 ![]() 表示双曲线”.
表示双曲线”.
(1)若“p且q”是真命题,求m的取值范围;
(2)若q是s的必要不充分条件,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com