
椭圆 的两个焦点F1、F2,点P在椭圆C上,且PF1⊥F1F2,,|PF1|=
的两个焦点F1、F2,点P在椭圆C上,且PF1⊥F1F2,,|PF1|= ,
,
|PF2|=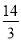 .
.
(1)求椭圆C的方程;
(2)若直线L过圆(x+2)2+(y-1)2=5的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线L的方程。
(1) ;(2)8x-9y+25=0
;(2)8x-9y+25=0
【解析】
试题分析:(1)由椭圆的定义可知a=3,在Rt△PF1F2中,由勾股定理得c= ,从而b2=4, 所以椭圆C的方程为
,从而b2=4, 所以椭圆C的方程为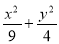 =1;(2) 法一:(韦达定理)设直线l的方程为y=k(x+2)+1,代入椭圆C的方程并化简得
=1;(2) 法一:(韦达定理)设直线l的方程为y=k(x+2)+1,代入椭圆C的方程并化简得
(4+9k2)x2+(36k2+18k)x+36k2+36k-27=0.由A,B关于点M对称可得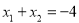 ,结合韦达定理可得
,结合韦达定理可得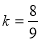 ,所以直线l的方程为8x-9y+25=0.(经检验,符合题意)法二:(点差求斜率)因为A、B关于点M对称,所以x1+ x2=-4, y1+ y2=2,由题意x1
,所以直线l的方程为8x-9y+25=0.(经检验,符合题意)法二:(点差求斜率)因为A、B关于点M对称,所以x1+ x2=-4, y1+ y2=2,由题意x1 x2且A、B的坐标满足椭圆方程,两式相减得直线l的斜率
x2且A、B的坐标满足椭圆方程,两式相减得直线l的斜率 ,因此直线l的方程为8x-9y+25=0.(经检验,符合题意.)
,因此直线l的方程为8x-9y+25=0.(经检验,符合题意.)
试题解析:(1)因为点P在椭圆C上,所以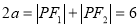 ,a=3. 在Rt△PF1F2中,
,a=3. 在Rt△PF1F2中,
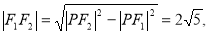 故椭圆的半焦距c=
故椭圆的半焦距c= ,从而b2=a2-c2=4,
,从而b2=a2-c2=4,
所以椭圆C的方程为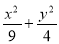 =1.
=1.
法一:设A,B的坐标分别为(x1,y1)、(x2,y2),由圆的方程为(x+2)2+(y-1)2=5,所以圆心M的坐标为(-2,1),从而可设直线l的方程为 y=k(x+2)+1,
代入椭圆C的方程得 (4+9k2)x2+(36k2+18k)x+36k2+36k-27=0.
因为A,B关于点M对称. 所以 解得
解得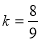 ,
,
所以直线l的方程为 即8x-9y+25=0. (经检验,符合题意)
即8x-9y+25=0. (经检验,符合题意)
法二:已知圆的方程为(x+2)2+(y-1)2=5,所以圆心M的坐标为(-2,1).
设A,B的坐标分别为(x1,y1),(x2,y2).由题意x1 x2且
x2且
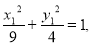 ①
① 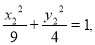 ②
②
由①-②得 ③
③
因为A、B关于点M对称,所以x1+ x2=-4, y1+ y2=2, 代入③得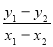 =
= ,即直线l的斜率为
,即直线l的斜率为 ,所以直线l的方程为y-1=
,所以直线l的方程为y-1= (x+2),即8x-9y+25=0.(经检验,所求直线方程符合题意.)
(x+2),即8x-9y+25=0.(经检验,所求直线方程符合题意.)
考点:1.椭圆的定义与方程;2.直线与椭圆的位置关系


科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标1.1练习卷(解析版) 题型:填空题
从集合{1,2,3,…,10}中任意选出三个不同的数,使这三个数成等比数列,这样的等比数列的个数为________.
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
具有性质: =-f(x)的函数,我们称为满足“倒负”变换的函数,下列函数:
=-f(x)的函数,我们称为满足“倒负”变换的函数,下列函数:
①y=x- ;②y=x+
;②y=x+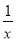 ;③y=
;③y=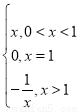 ,其中满足“倒负”变换的函数是( )
,其中满足“倒负”变换的函数是( )
A.①② B.①③ C.②③ D.①
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
有下列四个命题:
①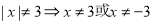 ;
;
②命题“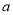 、
、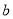 都是偶数,则
都是偶数,则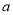 +
+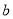 是偶数”的逆否命题是“
是偶数”的逆否命题是“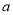 +
+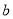 不是偶数,则
不是偶数,则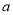 、
、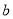 都不是偶数”;
都不是偶数”;
③若有命题p:7≥7,q:ln2>0, 则p且q是真命题;
④若一个命题的否命题为真,则它的逆命题一定是真. 其中真命题为( )
A.①④ B.②③ C.②④ D.③④
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二上学期期中考试理科数学试卷(解析版) 题型:填空题
若点A的坐标为(3,2),F为抛物线 的焦点,点P是抛物线上的一动点,则
的焦点,点P是抛物线上的一动点,则 取得最小值时,点P的坐标是 。
取得最小值时,点P的坐标是 。
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二上学期期中考试理科数学试卷(解析版) 题型:选择题
从装有3个红球、2个白球的袋中任取3个球,则所取的3个球中至少有1个白球的概率是( )
A.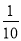 B.
B.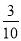 C.
C. D.
D.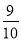
查看答案和解析>>
科目:高中数学 来源:2015届福建省高二下学期期末考试理科数学试卷(解析版) 题型:解答题
在直角坐标系 中,以O为极点,
中,以O为极点,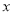 轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为
轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为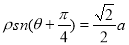 ,曲线
,曲线 的参数方程为
的参数方程为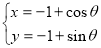 ,(
,(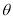 为参数,
为参数,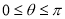 )。
)。
(Ⅰ)求C1的直角坐标方程;
(Ⅱ)当C1与C2有两个公共点时,求实数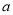 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com