
已知 ,若
,若 ,则
,则 .
.
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:填空题
已知函数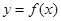 是
是 上的偶函数,对任意
上的偶函数,对任意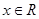 ,都有
,都有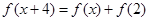 成立,当
成立,当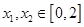 且
且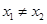 时,都有
时,都有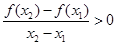 给出下列命题:
给出下列命题:
①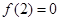 且
且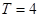 是函数
是函数 的一个周期;②直线
的一个周期;②直线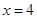 是函数
是函数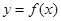 的一条对称轴;
的一条对称轴;
③函数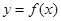 在
在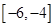 上是增函数; ④函数
上是增函数; ④函数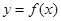 在
在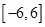 上有四个零点.其中正确命题的序号为 (把所有正确命题的序号都填上)
上有四个零点.其中正确命题的序号为 (把所有正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
若一系列函数的解析式相同,值域相同,但定义域不同,则我们称这些函数为“孪生函数”,那么解析式为 ,值域为
,值域为 的“孪生函数”共有___________个.
的“孪生函数”共有___________个.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
某同学在研究函数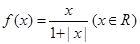 时,分别给出下面几个结论:
时,分别给出下面几个结论:
①等式 对
对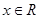 恒成立; ②函数
恒成立; ②函数 的值域为
的值域为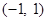 ;
;
③若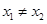 ,则一定有
,则一定有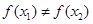 ; ④函数
; ④函数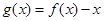 在
在 上有三个零点。 其中正确结论的序号有____________.
上有三个零点。 其中正确结论的序号有____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com