
【题目】(本小题满分13分)
已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)证明: ![]() 在区间
在区间![]() 上恰有
上恰有![]() 个零点.
个零点.
【答案】(1)![]() (2)详见解析
(2)详见解析
【解析】试题分析:(Ⅰ)当![]() 时,
时, ![]() ,求出
,求出![]() 的值可得切点坐标,求出
的值可得切点坐标,求出![]() 的值可得切线斜率,由点斜式可得曲线
的值可得切线斜率,由点斜式可得曲线![]() 在点
在点![]() 处的切线方程;(Ⅱ)求出导函数
处的切线方程;(Ⅱ)求出导函数![]() .由
.由 ![]() ,得
,得 ![]() .根据零点存在定理可得存在唯一的
.根据零点存在定理可得存在唯一的![]() , 使得
, 使得 ![]() ,
, ![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.可证明
上单调递减.可证明![]() ,从而可得结论.
,从而可得结论.
试题解析:(Ⅰ)当![]() 时,
时, ![]() ,
,
所以 ![]() .
.
因为 ![]() ,
, ![]() ,
,
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅱ)![]() .
.
由 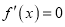 ,得
,得 ![]() .
.
因为 ![]() ,所以
,所以![]() .
.
当 ![]() 时, 由
时, 由 ![]() , 得
, 得 ![]() .
.
所以 存在唯一的![]() , 使得
, 使得 ![]() .
.
![]() 与
与![]() 在区间
在区间![]() 上的情况如下:
上的情况如下:
|
|
|
|
|
|
|
|
| ↗ | 极大值 | ↘ |
所以 ![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.
上单调递减.
因为 ![]() ,
,
且 ![]() ,
,
所以 ![]() 在区间
在区间![]() 上恰有2个零点.
上恰有2个零点.
【方法点晴】本题主要考查利用导数求曲线切线方程以及利用导数研究函数的单调性与极值,属于难题.求曲线切线方程的一般步骤是:(1)求出![]() 在
在![]() 处的导数,即
处的导数,即![]() 在点
在点![]()
![]() 出的切线斜率(当曲线
出的切线斜率(当曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行时,在 处导数不存在,切线方程为
轴平行时,在 处导数不存在,切线方程为![]() );(2)由点斜式求得切线方程
);(2)由点斜式求得切线方程![]() .
.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】(导学号:05856312)[选修4-5:不等式选讲]
已知函数f(x)=|x-m|-2|x-1|(m∈R).
(Ⅰ)当m=3时,求函数f(x)的最大值;
(Ⅱ)解关于x的不等式f(x)≥0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的焦点为
的焦点为![]() ,椭圆
,椭圆![]() 的中心在原点,
的中心在原点,![]() 为其右焦点,点
为其右焦点,点![]() 为曲线
为曲线![]() 和
和![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为抛物线
为抛物线![]() 上的两个动点,且使得线段
上的两个动点,且使得线段![]() 的中点
的中点![]() 在直线
在直线![]() 上,
上,
![]() 为定点,求
为定点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】老师在四个不同的盒子里面放了4张不同的扑克牌,分别是红桃![]() ,梅花
,梅花![]() ,方片
,方片![]() 以及黑桃
以及黑桃![]() ,让明、小红、小张、小李四个人进行猜测:
,让明、小红、小张、小李四个人进行猜测:
小明说:第1个盒子里面放的是梅花![]() ,第3个盒子里面放的是方片
,第3个盒子里面放的是方片![]() ;
;
小红说:第2个盒子里面饭的是梅花![]() ,第3个盒子里放的是黑桃
,第3个盒子里放的是黑桃![]() ;
;
小张说:第4个盒子里面放的是黑桃![]() ,第2个盒子里面放的是方片
,第2个盒子里面放的是方片![]() ;
;
小李说:第4个盒子里面放的是红桃![]() ,第3个盒子里面放的是方片
,第3个盒子里面放的是方片![]() ;
;
老师说:“小明、小红、小张、小李,你们都只说对了一半.”则可以推测,第4个盒子里装的是( )
A. 红桃![]() 或黑桃
或黑桃![]() B. 红桃
B. 红桃![]() 或梅花
或梅花![]()
C. 黑桃![]() 或方片
或方片![]() D. 黑桃
D. 黑桃![]() 或梅花
或梅花![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是菱形的四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 分别为
分别为![]() 的中点,设直线
的中点,设直线![]() 与平面
与平面![]() 交于点
交于点![]() .
.

(1)已知平面![]() 平面
平面![]() ,求证:
,求证: ![]() .
.
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在区间(-∞,+∞)上且以2为周期的函数,对k∈Z,用Ik表示区间(2k-1,2k+1),已知当x∈I0时,f(x)=x2.求f(x)在Ik上的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且f(0)=0,当x>0时,
f(x)=![]() .
.
(1)求函数f(x)的解析式;
(2)解不等式f(x2-1)>-2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的点,且
上的点,且![]() ,沿
,沿![]() 将
将![]() 折起并连接成如图的多面体
折起并连接成如图的多面体![]() ,折后
,折后![]() .
.
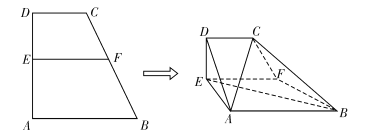
(Ⅰ)求证: ![]() ;
;
(Ⅱ)若折后直线![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦值是
的正弦值是![]() ,求证:平面
,求证:平面![]() 平面
平面![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com