
【题目】已知函数![]() .(
.( ![]() )
)
(I)试确定函数![]() 的零点个数;
的零点个数;
(II)设![]() 是函数
是函数![]() 的两个零点,当
的两个零点,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(I)函数![]() 的零点即方程
的零点即方程![]() 的根,变形为
的根,变形为![]() ,令
,令![]() ,根据图像特征讨论即可;
,根据图像特征讨论即可;
(II)根据![]() 是函数
是函数![]() 的两个零点,得
的两个零点,得![]() (
(![]() ),
),![]() (
(![]() ),得
),得![]()
![]()
![]()
 ,进而利用
,进而利用![]() 求范围即可.
求范围即可.
试题解析:

解法1:(I)函数![]() 的零点即方程
的零点即方程![]() 的根,
的根,
由![]() 得
得![]() ,令
,令![]() ,
,
则![]() ,--------------------2分
,--------------------2分
由![]() 得
得![]() ,∴函数
,∴函数![]() 在
在![]() 单调递增,
单调递增,
由![]() 得
得![]() ,∴函数
,∴函数![]() 在
在![]() 上单调递减,----3分
上单调递减,----3分
∴当![]() 时,函数
时,函数![]() 有最大值,
有最大值, ![]() ,
,
又当![]() 时,
时, ![]() >0,当
>0,当![]() 时
时![]() ;
;
当![]() 时
时![]() >0,
>0, ![]() ,当
,当![]() 时
时![]() ,
,
∴当![]() 时,
时, ![]() 与
与![]() 只有一个公共点,从而函数
只有一个公共点,从而函数![]() 有一个零点;
有一个零点;
当![]() 时,
时, ![]() 与
与![]() 有两个公共点,从而函数
有两个公共点,从而函数![]() 有两个零点.
有两个零点.
(II)设![]() 由(I)知
由(I)知![]() 且
且![]() ,
,
由![]() ,得
,得![]() (
(![]() )
)
由![]() ,得
,得![]() (
(![]() )
)
∴![]()
![]()
![]()
 ,
,
∵![]() ∴
∴![]() ,
, ![]() ,(两者仅当
,(两者仅当![]() 时取等号)
时取等号)
∴![]() ,又
,又![]() ,
,
∴ ,
,
∴![]() ,
,
由![]() 得
得![]() .
.
解法2:(I)∵![]() ,
, ![]() 不是函数的零点;
不是函数的零点;
当![]() 时,由
时,由![]() 得
得![]()
设![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 和
和![]() 上单调递减,
上单调递减,
当![]() 且
且![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ;
;
当![]() 且
且![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ;
;
当![]() 时,由
时,由![]() ,有
,有![]() ,
,
当![]() 时,有
时,有![]() ,
, ![]() ,
,
所以当![]() 时,曲线
时,曲线![]() 与
与![]() 只一个公共点,函数
只一个公共点,函数![]() 有一个零点;
有一个零点;
当![]() 时,曲线
时,曲线![]() 与
与![]() 有两个公共点,函数
有两个公共点,函数![]() 有两个零点;
有两个零点;
(II)不妨设![]() ,由(I)得
,由(I)得![]() ,且
,且![]() ,
, ![]() ,
,
由![]() ,
, ![]() ,得
,得![]() ,
, ![]() ,
,
∴![]()
![]()
![]()
 ,
,
∵![]() ∴
∴![]() ,
, ![]() ,(两者仅当
,(两者仅当![]() 时取等号)
时取等号)
∴![]() ,又
,又![]() ,
,
∴ ,
,
∴![]() ,由
,由![]() 得
得![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】某手机生产企业为了解消费者对某款手机功能的认同情况,通过销售部随机抽取50名购买该款手机的消费者,并发出问卷调查(满分50分),该问卷只有30份给予回复,这30份的评分如下:

(Ⅰ)完成下面的茎叶图,并求16名男消费者评分的中位数与14名女消费者评分的平均值;
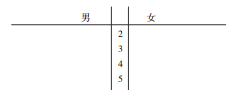

(Ⅱ)若大于40分为“满意”,否则为“不满意”,完成上面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为消费者对该款手机的“满意度”与性别有关.
的把握认为消费者对该款手机的“满意度”与性别有关.
参考公式:  ,其中
,其中![]()
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于二项式(x-1)2005有下列命题:
①该二项展开式中非常数项的系数和是1;
②该二项展开式中第六项为![]() x1999;
x1999;
③该二项展开式中系数最大的项是第1002项;
④当x=2006时,(x-1)2005除以2006的余数是2005。
其中正确命题的序号是__________。(注:把你认为正确的命题序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
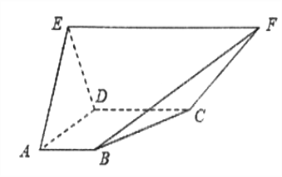
【题目】(本小题满分12分)在如图所示的五面体中,面![]() 为直角梯形,
为直角梯形, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是边长为2的正三角形.
是边长为2的正三角形.
(1)证明: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张同学计划在期末考试结束后,和其他小伙伴一块儿外出旅游,增长见识.旅行社为他们提供了省内的都江堰、峨眉山、九寨沟和省外的丽江古城,黄果树瀑布和凤凰古城这六个景点,由于时间和距离等原因,只能从中任取4个景点进行参观,其中黄果树瀑布不能第一个参观,且最后参观的是省内景点,则不同的旅游顺序有( )
A. 54种 B. 72种 C. 120种 D. 144种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在 ![]() 上的函数
上的函数 ![]() 若同时满足:①存在
若同时满足:①存在 ![]() ,使得对任意的
,使得对任意的 ![]() ,都有
,都有 ![]() ;②
;② ![]() 的图象存在对称中心.则称
的图象存在对称中心.则称 ![]() 为“
为“![]() 函数”.已知函数
函数”.已知函数 ![]() 和
和 ![]() ,则以下结论一定正确的是
,则以下结论一定正确的是 ![]()
A. ![]() 和
和 ![]() 都是
都是 ![]() 函数 B.
函数 B. ![]() 是
是 ![]() 函数,
函数, ![]() 不是
不是 ![]() 函数
函数
C. ![]() 不是
不是 ![]() 函数,
函数, ![]() 是
是 ![]() 函数 D.
函数 D. ![]() 和
和 ![]() 都不是
都不是 ![]() 函数
函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com