
【题目】如图,在直三棱柱![]() 中,
中, ![]() 为
为![]() 上的点,
上的点, ![]() 平面
平面![]() ;
;
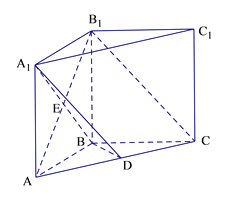
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,且
,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)连结![]() ,证明
,证明![]() ,即可证明
,即可证明![]() 平面
平面![]() .
.
(Ⅱ)建立空间直角坐标系,利用向量求解即可.
试题解析:

(Ⅰ)连结ED,
∵平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() 为
为![]() 中点,∴
中点,∴![]() 为
为![]() 中点,
中点,
∵![]() , ∴
, ∴![]() ①,
①,
法一:由![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,得
,得![]() ②,
②,
由①②及![]() 是平面
是平面![]() 内的两条相交直线,
内的两条相交直线,
得![]() 平面
平面![]() .
.
【法二:由![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
∴平面![]() ⊥平面
⊥平面![]() ,又平面
,又平面![]()
![]() 平面
平面![]() ,得
,得![]() 平面
平面![]() .】
.】
(Ⅱ)由![]() 得
得![]() ,
,
由(Ⅰ)知![]() ,又
,又![]() 得
得![]() ,
,
∵![]() ,∴
,∴![]() ,
,
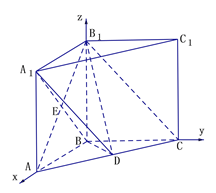
如图以B为原点,建立空间直角坐标系![]() 如图示,
如图示,
则![]() ,
, ![]() ,
, ![]() ,
,
得![]() ,
, ![]() ,
,
设![]() 是平面A1B1D的一个法向量,
是平面A1B1D的一个法向量,
则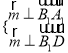 ,得
,得 ,令z=1,得
,令z=1,得![]() ,
,
设![]() 为平面A1BD的一个法向量,则
为平面A1BD的一个法向量,则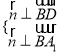 ,得
,得 ,
,
令![]() 得
得![]() ,
,
依题意知二面角![]() 为锐二面角,设其大小为
为锐二面角,设其大小为![]() ,
,
则 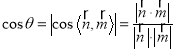
![]() ,
,
即二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某种药种植基地有两处种植区的药材需在下周一、周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘,由于下雨会影响药材的收益,若基地收益如下表所示:已知下周一和下周二无雨的概率相同且为![]() ,两天是否下雨互不影响,若两天都下雨的概率为
,两天是否下雨互不影响,若两天都下雨的概率为![]()

(1)求![]() 及基地的预期收益;
及基地的预期收益;
(2)若该基地额外聘请工人,可在周一当天完成全部采摘任务,若周一无雨时收益为![]() 万元,有雨时收益为
万元,有雨时收益为![]() 万元,且额外聘请工人的成本为
万元,且额外聘请工人的成本为![]() 元,问该基地是否应该额外聘请工人,请说明理由.
元,问该基地是否应该额外聘请工人,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机厂商推出一次智能手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:

(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的方差大小(不计算具体值,给出结论即可);
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意取2名用户,求2名用户评分小于90分的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三(1)班全体女生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图所示,据此解答如下问题:

(1)求高三(1)班全体女生的人数;
(2)求分数在[80,90)之间的女生人数,并计算频率分布直方图中[80,90)之间的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析女生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入![]() 的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
8 | 3 | 4 |
1 | 5 | 9 |
6 | 7 | 2 |
A. 9 B. 8 C. 6 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n.如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验.
假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为![]() ,且各件产品是否为优质品相互独立.
,且各件产品是否为优质品相互独立.
(1)求这批产品通过检验的概率;
(2)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙同学参加学校“一站到底”闯关活动,活动规则:①依次闯关过程中,若闯关成功则继续答题;若没通关则被淘汰;②每人最多闯3关;③闯第一关得10分,闯第二关得20分,闯第三关得30分,一关都没过则没有得分.已知甲每次闯关成功的概率为![]() ,乙每次闯关成功的概率为
,乙每次闯关成功的概率为![]() .
.
(Ⅰ)设乙的得分总数为![]() ,求
,求![]() 得分布列和数学期望;
得分布列和数学期望;
(Ⅱ)求甲恰好比乙多30分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com