
���� ��1������C2�ļ����귽��lת��Ϊ��2+��2sin2��=8���ɴ����������C2��ֱ�����귽�̣�����C1�IJ���������ȥ����t�����������C1����ͨ���̣�
��2����A��x1��y1����B��x2��y2��������������$\left\{\begin{array}{l}{y=x-3}\\{{x}^{2}+2{y}^{2}=8}\end{array}\right.$����3x2-12x+10=0���ɴ�����Τ�ﶨ�����ҳ���ʽ�����|AB|��ֵ��
��� �⣺��1��������C2�ļ����귽��Ϊ��2��1+sin2�ȣ�=8��
����2+��2sin2��=8��
������C2��ֱ�����귽��Ϊx2+2y2=8��
������C1�IJ�������Ϊ$\left\{\begin{array}{l}x=1+\frac{{\sqrt{2}}}{2}t\\ y=-2+\frac{{\sqrt{2}}}{2}t\end{array}\right.$��tΪ��������
������C1��ȥ����t��������C1����ͨ����Ϊy=x-3��
��2��������C1��C2��������A��B������A��x1��y1����B��x2��y2����
����������$\left\{\begin{array}{l}{y=x-3}\\{{x}^{2}+2{y}^{2}=8}\end{array}\right.$����ȥy����x2+2��x-3��2=8��
��������3x2-12x+10=0����$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=4}\\{{x}_{1}{x}_{2}=\frac{10}{3}}\end{array}\right.$��
��|AB|=$\sqrt{��1+{1}^{2}����{x}_{1}-{x}_{2}��^{2}}$=$\sqrt{2}$•$\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$\frac{4\sqrt{3}}{3}$��
���� ���⿼�����ߵ���ͨ���̵��������ҳ���������ֱ�����귽�̡������귽�̡��������̵Ļ����Ȼ���֪ʶ������������֤����������������������黯����ת��˼�룬���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ҹ��ġ����顷�м���������������ϵĻ÷�����1��2������9���뷽���ڣ�ʹ���С����У������Խ��ߵ�������֮�Ͷ�����15����ͼ��ʾ��
�ҹ��ġ����顷�м���������������ϵĻ÷�����1��2������9���뷽���ڣ�ʹ���С����У������Խ��ߵ�������֮�Ͷ�����15����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
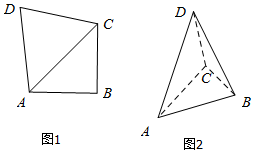 ��ͼ�����ı���ABCD�У�AB=BC=2����ABC=90�㣬DA=DC=$\sqrt{6}$�����ضԽ���AC����ʹ��ƽ��DAC��ƽ��ABC����ʱ��A��B��C��D��ͬһ�������ϣ�����������ǣ�������
��ͼ�����ı���ABCD�У�AB=BC=2����ABC=90�㣬DA=DC=$\sqrt{6}$�����ضԽ���AC����ʹ��ƽ��DAC��ƽ��ABC����ʱ��A��B��C��D��ͬһ�������ϣ�����������ǣ�������| A�� | $\frac{9}{2}��$ | B�� | $\frac{{8\sqrt{2}}}{3}��$ | C�� | $\frac{27}{2}��$ | D�� | 12�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A�� | 2.5% | B�� | 1% | C�� | 0.1% | D�� | 97.5% |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
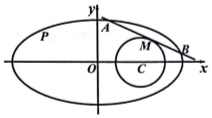 ��֪��Բ����Ϊ$\frac{{x}^{2}}{4}$+y2=1��ԲC����x-1��2+y2=r2��
��֪��Բ����Ϊ$\frac{{x}^{2}}{4}$+y2=1��ԲC����x-1��2+y2=r2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | �Ŀ� | �ϼ� | |
| �� | 13 | 10 | 23 |
| Ů | 7 | 20 | 27 |
| �ϼ� | 20 | 30 | 50 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��10��10�� | B�� | ��10��9�� | C�� | ��11��9�� | D�� | ��9��10�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com