
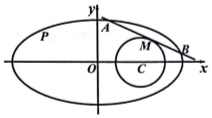
 已知椭圆方程为$\frac{{x}^{2}}{4}$+y2=1,圆C:(x-1)2+y2=r2.
已知椭圆方程为$\frac{{x}^{2}}{4}$+y2=1,圆C:(x-1)2+y2=r2.分析 (Ⅰ)利用两点之间的距离公式,根据x的取值范围,即可求得丨PC丨的最小值;
(Ⅱ)利用点差法求得直线AB的斜率,根据kMC×kAB=-1,求得M点坐标,由$\frac{{x}_{0}^{2}}{4}+{y}_{0}^{2}<1$,求得y02<$\frac{5}{9}$,由圆的方程,即可求得半径r的取值范围.
解答 解:(Ⅰ)设P(x,y),丨PC丨=$\sqrt{(x-1)^{2}+{y}^{2}}$=$\sqrt{\frac{3}{4}{x}^{2}-2x+2}$=$\sqrt{\frac{3}{4}(x-\frac{4}{3})^{2}+\frac{2}{3}}$,
由-2≤x≤2,当x=$\frac{4}{3}$时,丨PC丨min=$\frac{\sqrt{6}}{3}$,
(Ⅱ)当直线AB斜率不存在时且与椭圆C相切时,M在x轴上,
故满足条件的直线有两条;
当直线AB斜率存在时,设A(x1,y1),B(x2,y2),M(x0,y0),
由$\left\{\begin{array}{l}{\frac{{x}_{1}^{2}}{4}+{y}_{1}^{2}=1}\\{\frac{{x}_{2}^{2}}{4}+{y}_{2}^{2}=1}\end{array}\right.$,整理得:$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{1}{4}$×$\frac{{x}_{1}+{x}_{2}}{{y}_{1}+{y}_{2}}$,
则kAB=-$\frac{{x}_{0}}{4{y}_{0}}$,kMC=$\frac{{y}_{0}}{{x}_{0}-1}$,kMC×kAB=-1,
则kMC×kAB=-$\frac{{x}_{0}}{4{y}_{0}}$×$\frac{{y}_{0}}{{x}_{0}-1}$=-1,解得:x0=$\frac{4}{3}$,
由M在椭圆内部,则$\frac{{x}_{0}^{2}}{4}+{y}_{0}^{2}<1$,解得:y02<$\frac{5}{9}$,
由:r2=(x0-1)2+y02=$\frac{1}{9}$+y02,
∴$\frac{1}{9}$<r2<$\frac{2}{3}$,解得:$\frac{1}{3}$<r<$\frac{\sqrt{6}}{3}$.
∴半径r的取值范围($\frac{1}{3}$,$\frac{\sqrt{6}}{3}$).
点评 本题考查点差法的应用,两点直线的距离性质,二次函数的最值,考查计算能力,属于中档题.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:选择题
| A. | [10,15] | B. | [12,17] | C. | [13,17] | D. | [15,17] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | (-1)n | D. | (-1)n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$$\sqrt{5}$ | B. | 4$\sqrt{5}$ | C. | $\frac{8}{3}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20162 | B. | 2016×2017 | C. | 20172 | D. | 2017×2018 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3125 | B. | 5625 | C. | 8125 | D. | 0625 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com