
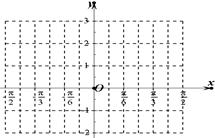
已知 .
.
(1)求 的最小值及取最小值时
的最小值及取最小值时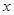 的集合;
的集合;
(2)求 在
在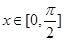 时的值域;
时的值域;
(3)在给出的直角坐标系中,请画出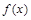 在区间
在区间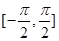 上的图像(要求列表,描点).
上的图像(要求列表,描点).
(1)当 ,
,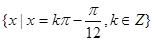 ;(2)
;(2)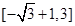 ;(3)详见解析.
;(3)详见解析.
解析试题分析:先根据平方差公式、同角三角函数的基本关系式、二倍角公式化简所给的函数
科目:高中数学
来源:
题型:解答题
已知函数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区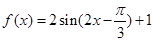 .(1)将
.(1)将 看成整体,然后由正弦函数
看成整体,然后由正弦函数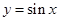 的最值可确定函数
的最值可确定函数 的最小值,并明确此时
的最小值,并明确此时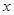 的值的集合;(2)先求出
的值的集合;(2)先求出 的范围为
的范围为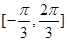 ,从而
,从而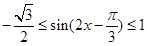 ,然后可求出
,然后可求出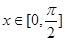 时,函数
时,函数 的值域;(3)根据正弦函数的五点作图法进行列表、描点、连线完成作图.
的值域;(3)根据正弦函数的五点作图法进行列表、描点、连线完成作图.
试题解析:化简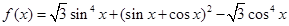
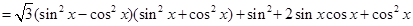
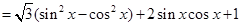
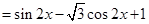
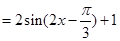 4分
4分
(1)当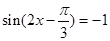 时,
时, 取得最小值
取得最小值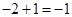 ,此时
,此时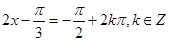 即
即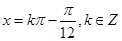 ,故此时
,故此时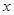 的集合为
的集合为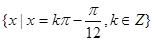 6分
6分
(2)当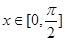 时,所以
时,所以 ,所以
,所以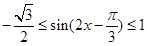 ,从而
,从而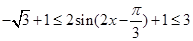 即
即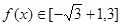 9分
9分
(3)由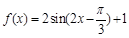 知
知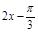
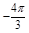
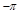
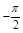
0 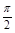
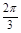
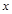
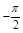
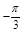
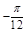
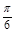

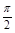
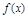


1加1阅读好卷系列答案
专项复习训练系列答案
初中语文教与学阅读系列答案

完形填空与阅读理解周秘计划系列答案
英语阅读理解150篇系列答案
奔腾英语系列答案
标准阅读系列答案
53English系列答案
考纲强化阅读系列答案
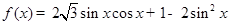 ,xÎR.
,xÎR.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)将函数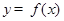 的图象上各点的纵坐标保持不变,横坐标先缩短到原来的
的图象上各点的纵坐标保持不变,横坐标先缩短到原来的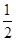 ,把所得到的图象再向左平移
,把所得到的图象再向左平移 单位,得到函数
单位,得到函数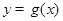 的图象,求函数
的图象,求函数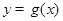 在区间
在区间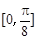 上的最小值.
上的最小值.
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号