
【题目】已知点F为椭圆![]() 的右焦点,点A为椭圆的右顶点.
的右焦点,点A为椭圆的右顶点.
(1)求过点F、A且和直线![]() 相切的圆C的方程;
相切的圆C的方程;
(2)过点F任作一条不与![]() 轴重合的直线
轴重合的直线![]() ,直线
,直线![]() 与椭圆交于P,Q两点,直线PA,QA分别与直线
与椭圆交于P,Q两点,直线PA,QA分别与直线![]() 相交于点M,N.试证明:以线段MN为直径的圆恒过点F.
相交于点M,N.试证明:以线段MN为直径的圆恒过点F.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
由已知可得![]() ,即可求出其中垂线
,即可求出其中垂线![]() ,即可得出半径为7,即可求出圆心坐标.即可写出圆C的方程.
,即可得出半径为7,即可求出圆心坐标.即可写出圆C的方程.
以线段MN为直径的圆恒过点![]() 等价于
等价于![]() ,讨论直线
,讨论直线![]() 的斜率是否存在,写出直线,联立解出P、Q,结合
的斜率是否存在,写出直线,联立解出P、Q,结合![]() 写出直线
写出直线![]() ,即可得到点M,N,结合
,即可得到点M,N,结合![]() ,即可说明
,即可说明![]() .
.
(1)由已知得:![]()
![]()
![]() 圆C的圆心一定在线段AF中垂线
圆C的圆心一定在线段AF中垂线![]() 上
上
由圆C与直线![]() 相切,得:圆C的半径
相切,得:圆C的半径![]()
设圆C的圆心坐标为![]() ,则有:
,则有:
![]() ,
,
即圆心![]()
![]() 圆C的方程为:
圆C的方程为:![]()
(2)证明:当直线![]() 斜率不存在时,其方程为
斜率不存在时,其方程为![]() ,
,
联立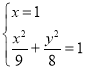 ,解得
,解得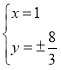 ,又因为
,又因为![]() .
.
所以直线![]() 为
为![]() .
.
可求得M,N两点坐标分别为![]() 或
或![]() ,又
,又![]()
![]() 的斜率之积为:
的斜率之积为:![]()
![]() .
.
当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() 的方程为:
的方程为:![]()
联立方程组: ,
,
消去![]() 整理得:
整理得:![]()
![]()
![]()
又设![]()
由P,A,M共线得:![]() ,
,
由Q,A,N共线得:![]() ,
,
所以FM,FN的斜率之积为:
![]()
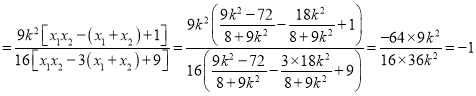
![]()
综上可知:恒有![]()
![]() 以线段MN为直径的圆恒过点F.
以线段MN为直径的圆恒过点F.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》中有一题:今有牛、马、羊食人苗,苗主责之粟四斗.羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?其意是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿4斗粟,羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比率偿还,牛、马、羊的主人各应赔偿多少粟?在这个问题中,牛主人比羊主人多赔偿了多少斗( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)求 函数![]() 的单调区间;
的单调区间;
(2)定义:对于函数![]() ,若存在
,若存在![]() ,使
,使![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的不动点. 如果函数
的不动点. 如果函数![]() 存在两个不同的不动点,求实数
存在两个不同的不动点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张上班从家到公司开车有两条线路,所需时间(分钟)随交通堵塞状况有所变化,其概率分布如下表所示:
所需时间(分钟) | 30 | 40 | 50 | 60 |
线路一 | 0.5 | 0.2 | 0.2 | 0.1 |
线路二 | 0.3 | 0.5 | 0.1 | 0.1 |
则下列说法正确的是( )
A.任选一条线路,“所需时间小于50分钟”与“所需时间为60分钟”是对立事件
B.从所需的平均时间看,线路一比线路二更节省时间
C.如果要求在45分钟以内从家赶到公司,小张应该走线路一
D.若小张上、下班走不同线路,则所需时间之和大于100分钟的概率为0.04
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.在做回归分析时,残差图中残差点分布的带状区域的宽度越窄表示回归效果越差
B.某地气象局预报:6月9日本地降水概率为90%,结果这天没下雨,这表明天气预报并不科学
C.回归分析模型中,残差平方和越小,说明模型的拟合效果越好
D.在回归直线方程![]() 中,当解释变量每增加1个单位时,预报变量多增加0.1个单位
中,当解释变量每增加1个单位时,预报变量多增加0.1个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为![]() (s为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(s为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,
,![]() ,直线与曲线C交于A,B两点.
,直线与曲线C交于A,B两点.
(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)已知点P的极坐标为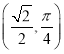 ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社会机构为了调查对手机游戏的兴趣与年龄的关系,通过问卷调查,整理数据得如下![]() 列联表:
列联表:
40岁以下 | 40岁以上 | 合计 | |
很兴趣 | 30 | 15 | 45 |
无兴趣 | 20 | 35 | 55 |
合计 | 50 | 50 | 100 |
(1)根据列联表,能否有![]() 的把握认为对手机游戏的兴趣程度与年龄有关?
的把握认为对手机游戏的兴趣程度与年龄有关?
(2)若已经从![]() 岁以下的被调查者中用分层抽样的方式抽取了
岁以下的被调查者中用分层抽样的方式抽取了![]() 名,现从这
名,现从这![]() 名被调查者中随机选取
名被调查者中随机选取![]() 名,求这
名,求这![]() 名被调查者中恰有
名被调查者中恰有![]() 名对手机游戏无兴趣的概率.
名对手机游戏无兴趣的概率.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.84 | 6.635 | 10.828 |
(注:参考公式: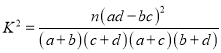 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就.在“杨辉三角”中,第![]() 行的所有数字之和为
行的所有数字之和为![]() ,若去除所有为1的项,依次构成数列
,若去除所有为1的项,依次构成数列![]() ,则此数列的前55项和为( )
,则此数列的前55项和为( )

A. 4072B. 2026C. 4096D. 2048
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线E的参数方程为![]() (
(![]() 为参数),以O为极点,x轴非负半轴为极轴建立极坐标系,直线
为参数),以O为极点,x轴非负半轴为极轴建立极坐标系,直线![]() ,
,![]() 的极坐标方程分别为
的极坐标方程分别为![]() ,
,![]() ,
,![]() 交曲线E于点A,B,
交曲线E于点A,B,![]() 交曲线E于点C,D.
交曲线E于点C,D.
(1)求曲线E的普通方程及极坐标方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com