Question

11．随机抽取某机器在一段时间内加工的零件100个，测量它们的直径，对这100个数据分组并统计各组的频数，其结果为[12.5，14.5），6；[14.5，16.5），16；[16.5，18.5），18；[18.5，20.5），22；[20.5，22.5），20；[22.5，24.5），10；[24.5，26.5），8．
（1）列出样本的频率分布表，并画出频率分布直方图；
（2）试估计这台机器加工一个这种零件的直径不小于20.5的概率．

Answer 1

分析 （1）由题中的所给数据，列成表格，即可得到频率分布表中的数据，由频率分布表中的数据，在横轴为数据，纵轴为$\frac{频率}{组距}$，即可得到频率分布直方图；
（2）为了估计数据小于20.5的概率，只须求出频率分步直方图中数据小于20.5的频率即可．

解答 解：（1）样本的频率分布表如下：

分组	频数	频率
[12.5，14.5）	6	0.06
[14.5，16.5）	16	0.16
[16.5，18.5）	18	0.18
[18.5，20.5）	22	0.22
[20.5，22.5）	20	0.20
[22.5，24.5）	10	0.10
[24.5，26.5）	8	0.08
合计	100	1.00

（2）频率分布直方图如下图．

（3）零件的直径不小于20.5的频率是$\frac{20+10+8}{100}$=0.38，
∴零件的直径不小于20.5的概率约为0.38．

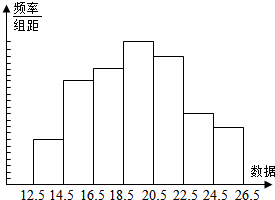
点评 解决总体分布估计问题的一般程序如下：（1）先确定分组的组数（最大数据与最小数据之差除组距得组数）；（2）分别计算各组的频数及频率（频率=$\frac{频率}{组距}$）；（3）画出频率分布直方图，并作出相应的估计．