
 在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“折线路径”,所有“折线路径”中长度最小的称为M到N的“折线距离”.如图所示的路径MD1D2D3N与路径MEN都是M到N的“折线路径”.某地有三个居民区分别位于平面xOy内三点A(-8,1),B(5,2),C(1,14),现计划在这个平面上某一点P(x,y)处修建一个超市.
在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“折线路径”,所有“折线路径”中长度最小的称为M到N的“折线距离”.如图所示的路径MD1D2D3N与路径MEN都是M到N的“折线路径”.某地有三个居民区分别位于平面xOy内三点A(-8,1),B(5,2),C(1,14),现计划在这个平面上某一点P(x,y)处修建一个超市.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
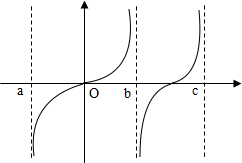 已知函数f(x),x∈(a,b)∪(b,c)的图象如图所示,有三个同学对此函数的单调性作出如下的判断:
已知函数f(x),x∈(a,b)∪(b,c)的图象如图所示,有三个同学对此函数的单调性作出如下的判断:查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an |
| 2n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| n |
| π |
| 3 |
| 3 |
| 7 |
2
| ||
| 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com