
【题目】已知函数f(x)=x2﹣2x(x∈[﹣1,2])的值域为集合A,g(x)=ax+2(x∈[﹣1,2])的值域为集合B.若AB,则实数a的取值范围是 .
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】定义:若两个二次曲线的离心率相等,则称这两个二次曲线相似.如图,椭圆C的中心在原点,焦点在x轴上,右顶点为A,以其短轴的两个端点B1 , B2及其一个焦点为顶点的三角形是边长为6的正三角形,M是C上异于B1 , B2的一个动点,△MB1B2的重心为G,G点的轨迹记为C1 . 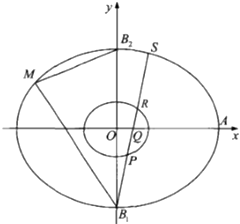
(1)(i)求C的方程;
(ii)求证:C1与C相似;
(2)过B1点任作一直线,自下至上依次与C1、x轴的正半轴、C交于不同的四个点P,Q,R,S,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知中心在原点,离心率为
中,已知中心在原点,离心率为![]() 的椭圆
的椭圆![]() 的一个焦点为圆
的一个焦点为圆![]() :
: ![]() 的圆心.
的圆心.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 是椭圆
是椭圆![]() 上一点,过
上一点,过![]() 作两条斜率之积为
作两条斜率之积为![]() 的直线
的直线![]() ,
, ![]() ,当直线
,当直线![]() ,
, ![]() 都与圆
都与圆![]() 相切时,求
相切时,求![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年袁隆平的超级杂交水稻再创亩产量世界纪录,为了测试水稻生长情况,专家选取了甲、乙两块地,从这两块地中随机各抽取
年袁隆平的超级杂交水稻再创亩产量世界纪录,为了测试水稻生长情况,专家选取了甲、乙两块地,从这两块地中随机各抽取![]() 株水稻样本,测量他们的高度,获得的高度数据的茎叶图如图所示:
株水稻样本,测量他们的高度,获得的高度数据的茎叶图如图所示:
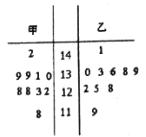
(1)根据茎叶图判断哪块田的平均高度较高;
(2)计算甲乙两块地株高方差;
(3)现从乙地高度不低于![]() 的样本中随机抽取两株,求高度为
的样本中随机抽取两株,求高度为![]() 的样本被抽中的概率.
的样本被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量x(万辆) | 50 | 51 | 54 | 57 | 58 |
PM2.5的浓度y(微克/立方米) | 69 | 70 | 74 | 78 | 79 |
(1)根据上表数据,请在如图坐标系中画出散点图; 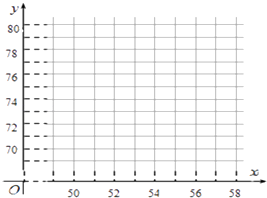
(2)根据上表数据,用最小二乘法求出y关于x的线性回归方程 ![]() ;(保留2位小数)
;(保留2位小数)
(3)若周六同一时间段车流量是25万辆,试根据(2)求出的线性回归方程预测,此时PM2.5的浓度为多少(保留整数)?
参考公式: ![]() =
= 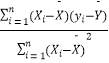 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国的烟花名目繁多,花色品种繁杂.其中“菊花”烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点时爆裂,通过研究,发现该型烟花爆裂时距地面的高度h(单位:米)与时间t(单位:秒)存在函数关系,并得到相关数据如下表:
时间t |
| 2 | 4 |
高度h | 10 | 25 | 17 |
( I)根据上表数据,从下列函数中,选取一个函数描述该型烟花爆裂时距地面的高度h与时间t的变化关系:y1=kt+b,y2=at2+bt+c,y3=abt , 确定此函数解析式,并简单说明理由;
( II)利用你选取的函数,判断烟花爆裂的最佳时刻,并求出此时烟花距地面的高度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两家快递公司其“快递小哥”的日工资方案如下:甲公司规定底薪![]() 元,每单抽成
元,每单抽成![]() 元;乙公司规定底薪
元;乙公司规定底薪![]() 元,每日前
元,每日前![]() 单无抽成,超过
单无抽成,超过![]() 单的部分每单抽成
单的部分每单抽成![]() 元
元
(1)设甲乙快递公司的“快递小哥”一日工资![]() (单位:元)与送货单数
(单位:元)与送货单数![]() 的函数关系式为
的函数关系式为![]() ,求
,求![]() ;
;
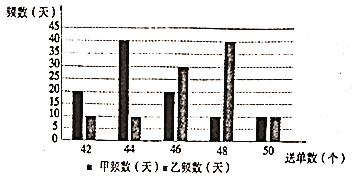
(2)假设同一公司的“快递小哥”一日送货单数相同,现从两家公司各随机抽取一名“快递小哥”,并记录其![]() 天的送货单数,得到如下条形图:
天的送货单数,得到如下条形图:
若将频率视为概率,回答下列问题:
①记乙快递公司的“快递小哥”日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小赵拟到两家公司中的一家应聘“快递小哥”的工作,如果仅从日收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2﹣a2x+3.
(1)若a=2,求f(x)在[﹣1,2]上的最值;
(2)若f(x)在(﹣ ![]() ,1)上是减函数,求a的取值范围.
,1)上是减函数,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com