
 ,3])的图象与直线y=m恰有三个交点,求实数m的取值范围;
,3])的图象与直线y=m恰有三个交点,求实数m的取值范围; f′(x)+alnx≤ax成立(其中f′(x)为函数f(x)的导函数),求实数a的取值范围.
f′(x)+alnx≤ax成立(其中f′(x)为函数f(x)的导函数),求实数a的取值范围. ,3]内的单调区间,找出函数在(-
,3]内的单调区间,找出函数在(- ,3)上的极值点,求出极值,把极值和端点处的函数值比较后,根据函数y=f(x)的图象与y=m恰有三个交点即可得到实数m的取值范围;
,3)上的极值点,求出极值,把极值和端点处的函数值比较后,根据函数y=f(x)的图象与y=m恰有三个交点即可得到实数m的取值范围; f′(x)+alnx≤ax成立,可转化为函数
f′(x)+alnx≤ax成立,可转化为函数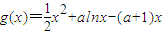 在[1,e]上的最小值小于等于0,求出函数g(x)的导函数,通过对a分类求解函数g(x)在[1,e]上的最小值,由最小值小于等于0求解实数a的取值范围.
在[1,e]上的最小值小于等于0,求出函数g(x)的导函数,通过对a分类求解函数g(x)在[1,e]上的最小值,由最小值小于等于0求解实数a的取值范围.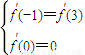 ,即
,即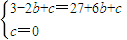 ,解得:
,解得: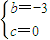 .
. ,(2,3]上递增,在(0,2)上递减.
,(2,3]上递增,在(0,2)上递减.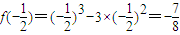 ,f(0)=0,f(2)=23-3×22=-4,f(3)=33-3×32=0.
,f(0)=0,f(2)=23-3×22=-4,f(3)=33-3×32=0. ,3])的图象与直线y=m恰有三个交点,则
,3])的图象与直线y=m恰有三个交点,则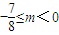 .
.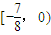 .
. f′(x)+alnx≤ax成立,即
f′(x)+alnx≤ax成立,即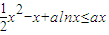 成立,
成立, ,则g(x)min≤0,
,则g(x)min≤0,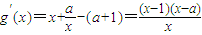 ,
,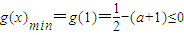 ,得
,得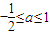 .
.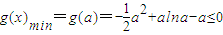 恒成立,∴1<a<e.
恒成立,∴1<a<e.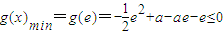 ,∴
,∴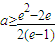 ,又
,又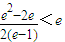 ,
,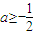 .
. ,+∞).
,+∞). f′(x)+alnx≤ax成立转化为一个函数的最小值小于等于0,考查了学生灵活分析和处理问题的能力.此题属难题.
f′(x)+alnx≤ax成立转化为一个函数的最小值小于等于0,考查了学生灵活分析和处理问题的能力.此题属难题. 

科目:高中数学 来源: 题型:
| 1 |
| 3 |
| f′(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:深圳一模 题型:解答题
| 1 |
| 3 |
| f′(x) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com