练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知f（x）=a （a＞0且a≠1），若f（lga）= ，则a= ．

    【答案】10或
    【解析】解：因为函数f（x）= （a＞0且a≠1），
    所以f（lga）= = ，
    两边取以10为底的对数，得：（lga﹣ ）lga= ，
    解得：lga=1或lga=﹣ ，
    ∴a=10或a=
    所以答案是：10或 ．
    【考点精析】本题主要考查了函数的零点与方程根的关系的相关知识点，需要掌握二次函数的零点：（1）△＞0，方程 有两不等实根，二次函数的图象与 轴有两个交点，二次函数有两个零点;（2）△＝0，方程 有两相等实根（二重根），二次函数的图象与 轴有一个交点，二次函数有一个二重零点或二阶零点;（3）△＜0，方程 无实根，二次函数的图象与 轴无交点，二次函数无零点才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】一次测验共有4个选择题和2个填空题，每答对一个选择题得20分，每答对一个填空题得10分，答错或不答得0分，若某同学答对每个选择题的概率均为 ，答对每个填空题的概率均为 ，且每个题答对与否互不影响．
    （1）求该同学得80分的概率；
    （2）若该同学已经答对了3个选择题和1个填空题，记他这次测验的得分为ξ，求ξ的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： 过点， 为椭圆的半焦距，且，过点作两条互相垂直的直线， 与椭圆分别交于另两点， ．

    （1）求椭圆的方程；

    （2）若直线的斜率为，求的面积；

    （3）若线段的中点在轴上，求直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

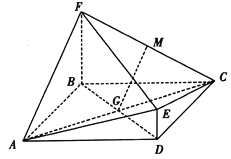
    【题目】如图，菱与四边形BDEF相交于BD， 平面ABCD，DE//BF,BF=2DE，AF⊥FC，M为CF的中点， ．

    (I)求证：GM／／平面CDE；

    (II)求证：平面ACE⊥平面ACF．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】己知函数 (其中e为自然对数的底数)， ．

    (I)求函数的单调区间；

    (II)设，.已知直线是曲线的切线，且函数上是增函数．

    (i)求实数的值；

    (ii)求实数c的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】己知函数， ．

    (I)求函数的单调区间；

    (II)设，已知函数在上是增函数．

    (1)研究函数上零点的个数；

    (ii)求实数c的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设p：实数x满足x2﹣4ax+3a2＜0，其中a＞0，命题q：实数x满足 ．
    （1）若a=1，且p∨q为真，求实数x的取值范围；
    （2）若p是q的必要不充分要条件，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4:坐标系与参数方程

    在直角坐标系中，圆的参数方程为（为参数），以O为极点， 轴的非负半轴为极轴建立极坐标系.

    （Ⅰ）求圆的普通方程；

    （Ⅱ）直线的极坐标方程是，射线与圆C的交点为，与直线的交点为，求线段的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列{an}的前n项和为Sn ， 且a1+a3=10，S4=24．
    （1）求数列{an}的通项公式；
    （2）令Tn= ，求证：Tn＜ ．

    查看答案和解析>>

    同步练习册答案