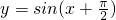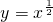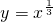Question

下列函数中既是偶函数，又是其定义域上的周期函数的是

1. A.
   
2. B.
   
3. C.
   
4. D.
   y=x^-3

Answer 1

A
分析：根据函数的奇偶性的定义判断各个选项中的函数是否为偶函数，结合函数的周期性，得出结论．
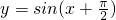
解答：∵=cosx，定义域为R，此函数为偶函数，且还是周期等于2的周期函数，故满足条件．
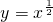
由于函数=的定义域为[0，+∞），不关于原点对称，不是偶函数，也不是周期函数，故不满足条件．
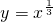
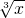
由于函数= 的定义域为R，是奇函数，不是周期函数，故不满足条件．
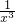
由于函数 y=x^-3= 定义域为{x|x≠0}，是奇函数，不是周期函数，故不满足条件，
故选A．
点评：本题主要考查函数的周期性以及求法，诱导公式，函数的奇偶性的定义和判断，属于中档题．