
如图,矩形ABCD中,AB=2,BC=2![]() ,以AC为轴翻折半平面,使二平面角B—AC—D为120°,求:(1)翻折后,D到平面ABC的距离;(2)BD和AC所成的角.
,以AC为轴翻折半平面,使二平面角B—AC—D为120°,求:(1)翻折后,D到平面ABC的距离;(2)BD和AC所成的角.
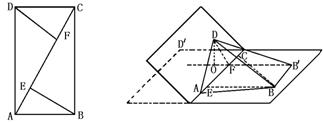
研究翻折问题,通常要画出翻折前的平面图形和翻折后的空间图形,对应点的字母要相同.
解 分别过B、D作AC的垂线,垂足是E、F,过F作FB′∥BE,过B作BB′∥AC,交点B′,则四边形EFB′B是矩形.
∵AC⊥DF,AC⊥B′F,∴AC⊥平面B′FD,即∠DF′B就是二面角B—AC—D的平面角,亦即∠DFB′=120°.
过D作DO⊥B′F,垂足为O.∵DO![]() 平面DFB′,AC⊥平面DFB′.∴DO⊥AF,DO⊥平面ABC.
平面DFB′,AC⊥平面DFB′.∴DO⊥AF,DO⊥平面ABC.
在RtΔADC中,CD=2,AD=2![]() ,∴DF=
,∴DF=![]() ,OD=DF·sin60°=
,OD=DF·sin60°=![]() .
.
(2)在ΔDFB′中,DB′=![]() =3.
=3.
又由(1)可知,AC∥BB′,AC⊥平面DFB′⊥平面DFB′.∴BB′⊥平面DFB′,∴ΔDB B′是直角三角形,又BB′=EF=2.∴tan∠DBB′=![]() .
.
∵AC∥BB′,∴AC与BD所成的角就是∠DBB′,即为arctan![]() .
.
说明 处理翻折问题,只要过不在棱上的点作棱的垂直相交的线段,就可以化成基本题型处理,本题也可以这样考虑,即利用异面直线DF、BE上两点B、D间的距离,先求出BD2=EF2+DF2+BE2-2DF·BE·cos120°=13,从而得出∠DBB′=arccos![]() .
.


科目:高中数学 来源: 题型:
 如图,矩形ABCD中,AB=
如图,矩形ABCD中,AB=8
| ||
| 3 |
| 2π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 A 若方程ax-x-a=0有两个实数解,则a的取值范围是
A 若方程ax-x-a=0有两个实数解,则a的取值范围是| AE |
| AF |
| 9 |
| 2 |
| 9 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,矩形ABCD中,DC=
如图,矩形ABCD中,DC=| 3 |
2
| ||||
| 12 |
2
| ||||
| 12 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (理)如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD
(理)如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD| PQ |
| QD |
| BP |
| QD |
| ||
| 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com