
| A. | $\frac{2-\sqrt{2}}{5}$ | B. | $\frac{2±\sqrt{2}}{5}$ | C. | $\frac{3-\sqrt{5}}{2}$ | D. | $\frac{3±\sqrt{5}}{2}$ |
分析 作出不等式组对应的平面区域,利用直线斜率公式,结合数形结合进行求解即可.
解答 解:作出不等式组对应的平面区域如图:
$\frac{y+1}{x}$的几何意义是区域内的点到定点D(0,-1)的斜率,
由图象知AD的斜率最小,
由$\left\{\begin{array}{l}{y=k}\\{x+y=4}\end{array}\right.$得$\left\{\begin{array}{l}{x=4-k}\\{y=k}\end{array}\right.$,得A(4-k,k),
则AD的斜率k=$\frac{k+1}{4-k}$,整理得k2-3k+1=0,
得k=$\frac{3-\sqrt{5}}{2}$或$\frac{3+\sqrt{5}}{2}$(舍),
故选:C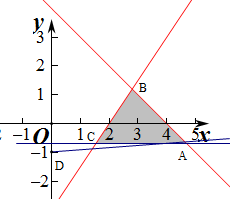
点评 本题主要考查线性规划的应用,结合直线的斜率公式,利用数形结合是解决本题的关键.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x∈(1,+∞),x3+16≤8x | B. | ¬p:?x∈(1,+∞),x3+16<8x | ||
| C. | ¬p:?x0∈(1,+∞),x03+16≤8x0 | D. | ¬p:?x0∈(1,+∞),x03+16<8x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,-2] | B. | [2,3] | C. | [-3,-2]∪{3} | D. | [2,3]∪{-3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
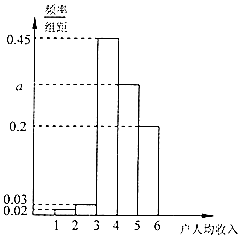 我国为确保贫困人口到2020年如期脱贫,把2017年列为“精准扶贫”攻坚年,2017年1月1日某贫困县随机抽取100户贫困家庭的每户人均收入数据做为样本,以考核该县2016年的“精准扶贫”成效(2016年贫困家庭脱贫的标准为人均收入不小于3000元).根据所得数据将人均收入(单位:千元)分成五个组:[1,2),[2,3),[3,4),[4,5),[5,6],并绘制成如图所示的频率分布直方图.
我国为确保贫困人口到2020年如期脱贫,把2017年列为“精准扶贫”攻坚年,2017年1月1日某贫困县随机抽取100户贫困家庭的每户人均收入数据做为样本,以考核该县2016年的“精准扶贫”成效(2016年贫困家庭脱贫的标准为人均收入不小于3000元).根据所得数据将人均收入(单位:千元)分成五个组:[1,2),[2,3),[3,4),[4,5),[5,6],并绘制成如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
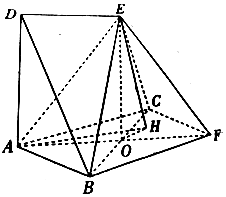 如图,边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直,AF∩BC=O,DE=$\sqrt{2}$,ED∥AF且∠DAF=90°
如图,边长为2的正方形ABFC和高为2的直角梯形ADEF所在的平面互相垂直,AF∩BC=O,DE=$\sqrt{2}$,ED∥AF且∠DAF=90°查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com