
【题目】已知函数f(x)= ![]() sinxcosx﹣cos2x+
sinxcosx﹣cos2x+ ![]() ,(x∈R).
,(x∈R).
(1)若对任意x∈[﹣ ![]() ,
, ![]() ],都有f(x)≥a,求a的取值范围;
],都有f(x)≥a,求a的取值范围;
(2)若先将y=f(x)的图象上每个点纵坐标不变,横坐标变为原来的2倍,然后再向左平移 ![]() 个单位得到函数y=g(x)的图象,求函数y=g(x)﹣
个单位得到函数y=g(x)的图象,求函数y=g(x)﹣ ![]() 在区间[﹣2π,4π]内的所有零点之和.
在区间[﹣2π,4π]内的所有零点之和.
【答案】
(1)解:函数f(x)= ![]() sinxcosx﹣cos2x+
sinxcosx﹣cos2x+ ![]()
= ![]() sin2x﹣
sin2x﹣ ![]() cos2x=sin(2x﹣
cos2x=sin(2x﹣ ![]() ),
),
若对任意x∈[﹣ ![]() ,
, ![]() ],都有f(x)≥a,
],都有f(x)≥a,
则只需 f(x)min≥a即可.
∵2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],故当2x﹣
],故当2x﹣ ![]() =﹣
=﹣ ![]() 时,
时,
f(x)min=﹣ ![]() ,故 a≤﹣
,故 a≤﹣ ![]() .
.
(2)解:若先将y=f(x)的图象上每个点纵坐标不变,
横坐标变为原来的2倍,可得y=sin(x﹣ ![]() )的图象;
)的图象;
然后再向左平移 ![]() 个单位得到函数y=g(x)=sinx的图象.
个单位得到函数y=g(x)=sinx的图象.
令g(x)﹣ ![]() =0,求得sinx=
=0,求得sinx= ![]() ,
,
求函数y=g(x)﹣ ![]() 在区间[﹣2π,4π]内的所有零点之和.
在区间[﹣2π,4π]内的所有零点之和.
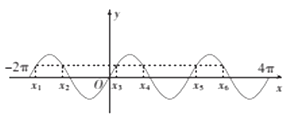
由图可知,sinx= ![]() 在区间[﹣2π,4π]内有6个零点:x1,x2,x3,x4,x5,x6,
在区间[﹣2π,4π]内有6个零点:x1,x2,x3,x4,x5,x6,
根据对称性有 ![]() =﹣
=﹣ ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
从而所有零点和为:x1+x2+x3+x4+x5+x6=3π.
【解析】(1)利用三角恒等变换化简f(x)的解析式,根据题意,x∈[﹣ ![]() ,
, ![]() ]时,f(x)min≥a.再利用正弦函数的定义域和值域,求得f(x)的最小值,可得a的范围.(2)根据函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,根据正弦函数的图象的对称性,求得函数y=g(x)﹣
]时,f(x)min≥a.再利用正弦函数的定义域和值域,求得f(x)的最小值,可得a的范围.(2)根据函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,根据正弦函数的图象的对称性,求得函数y=g(x)﹣ ![]() 在区间[﹣2π,4π]内的所有零点之和.
在区间[﹣2π,4π]内的所有零点之和.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】某工厂共有10台机器,生产一种仪器元件,由于受生产能力和技术水平等因素限制,会产生一定数量的次品.根据经验知道,若每台机器产生的次品数P(万件)与每台机器的日产量x(万件)(4≤x≤12)之间满足关系:P=0.1x2﹣3.2lnx+3,已知每生产1万件合格的元件可以盈利2万元,但每产生1万件装次品将亏损1万元.(利润=盈利﹣亏损) (I)试将该工厂每天生产这种元件所获得的利润y(万元)表示为x的函数;
(II)当每台机器的日产量x(万件)写为多少时所获得的利润最大,最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
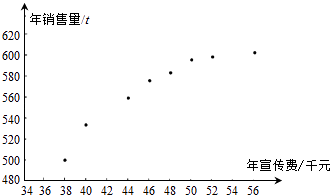
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响.对近8年的年宣传费xi和年销售量yi(i=1,2,,8)数据作了初步处理, 得到下面的散点图及一些统计量的值.
| | | | | | |
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
其中wi= ![]() ,
, ![]() =
= ![]()
(Ⅰ)根据散点图判断,y=a+bx与y=c+d ![]() 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利润z与x、y的关系为z=0.2y﹣x.根据(Ⅱ)的结果回答下列问题:
(i)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ii)年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据(u1 , v1),(u2 , v2),,(un , vn),其回归直线v=α+βμ的斜率和截距的最小二乘估计分别为: ![]() =
= 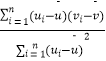 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量 ![]() =(sinx,
=(sinx, ![]() cosx),
cosx), ![]() =(﹣1,1),
=(﹣1,1), ![]() =(1,1),其中x∈(0,π].
=(1,1),其中x∈(0,π].
(1)若( ![]() +
+ ![]() )∥
)∥ ![]() ,求实数x的值;
,求实数x的值;
(2)若 ![]()
![]() =
= ![]() ,求函数sinx的值.
,求函数sinx的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按如图所示的程序框图操作: (Ⅰ)写出输出的数所组成的数集.若将输出的数按照输出的顺序从前往后依次排列,则得到数列{an},请写出数列{an}的通项公式;
(Ⅱ)如何变更A框内的赋值语句,使得根据这个程序框图所输出的数恰好是数列{2n}的前7项?
(Ⅲ)如何变更B框内的赋值语句,使得根据这个程序框图所输出的数恰好是数列{3n﹣2}的前7项?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x﹣8,g(x)=2x2﹣4x﹣16,
(1)求不等式g(x)<0的解集;
(2)若对一切x>2,均有f(x)≥(m+2)x﹣m﹣15成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)是定义在R上的奇函数,且在(﹣∞,0]上满足 ![]() <0,且f(1)=0,则使得
<0,且f(1)=0,则使得 ![]() <0的x的取值范围是( )
<0的x的取值范围是( )
A.(﹣∞,1)
B.(﹣∞,﹣1)∪(1,+∞)
C.(﹣1,0)∪(1,+∞)
D.(﹣1,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com