
����Ŀ��ij��������10̨����������һ������Ԫ�������������������ͼ���ˮƽ���������ƣ������һ�������Ĵ�Ʒ�����ݾ���֪������ÿ̨���������Ĵ�Ʒ��P���������ÿ̨�������ղ���x���������4��x��12��֮�������ϵ��P=0.1x2��3.2lnx+3����֪ÿ����1����ϸ��Ԫ������ӯ��2��Ԫ����ÿ����1���װ��Ʒ������1��Ԫ��������=ӯ�������� ��I���Խ��ù���ÿ����������Ԫ������õ�����y����Ԫ����ʾΪx�ĺ�����
��II����ÿ̨�������ղ���x�������дΪ����ʱ����õ���������������Ϊ���٣�
���𰸡��⣺��I�������⣬����õ�����Ϊ y=10[2��x��p����p]=10��2x��3p��=20x��30p=20x��3x2+96lnx��90��4��x��12��
��II���ɣ���y'=20��6x+ ![]() =
= ![]() ��
��
��y'=0���õ�x=6��x=�� ![]() ����ȥ����
����ȥ����
���Ե�4��x��6��y'��0��������[4��6]Ϊ����������6��x��12ʱ��y'��0�������ڣ�6��12��Ϊ��������
���Ե�x=6ʱ������ȥ����ֵ�������ֵ��
���Ե�x=6ʱ�������Ϊ20��6��3��62+96ln6��90=96ln6��78����Ԫ����
��ÿ̨�������ղ���Ϊ6�������ʱ����õ���������������Ϊ96ln6��78��Ԫ��
��������������������=ӯ�������𣬵õ�y��p�Ĺ�ϵ����p�����������ɣ����ԣ��Ľ���ʽ���ж�ȡ���ֵʱ��xֵ�����������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������Բ����һ���֣������ɾ���![]() �������ڲ�����
�������ڲ�����![]() ������ֱ��Ϊ��ת����ת
������ֱ��Ϊ��ת����ת![]() �õ��ģ�
�õ��ģ� ![]() ��
��![]() ���е�.
���е�.
��![]() ����
����![]() ��
��![]() �ϵ�һ�㣬��
�ϵ�һ�㣬��![]() ����
����![]() �Ĵ�С;
�Ĵ�С;
��![]() ����
����![]() ʱ,������
ʱ,������![]() �Ĵ�С.
�Ĵ�С.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��![]() �ķ���Ϊ
�ķ���Ϊ![]() ����
����![]() ��������
��������![]() �ϵ�ֱ��
�ϵ�ֱ��![]() ������С�ĵ㣬��
������С�ĵ㣬��![]() �������������ڵ�
�������������ڵ�![]() �ĵ㣬ֱ��
�ĵ㣬ֱ��![]() ��ֱ��
��ֱ��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ��ƽ�е�ֱ����������
��ƽ�е�ֱ����������![]() ���ڵ�
���ڵ�![]() .
.
�������![]() �����ꣻ
�����ꣻ
����֤��ֱ��![]() ������㣬����������������.
������㣬����������������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=1�� ![]()
��1������f��x���Ķ������ֵ��
��2�����жϺ���f��x������ż�ԣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����{an}������a1=3���ҹ���d��0����ǰn���ΪSn �� ��a1 �� a4 �� a13�ֱ��ǵȱ�����{bn}��b2 �� b3 �� b4 �� ����������{an}��{bn}��ͨ�ʽ��
����֤�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����λѧ���μ�ij�����ѵ������ѵ�ڼ䣬���Dzμӵ�5��Ԥ���ɼ��ľ�Ҷͼ��¼���£�
(1)�Ӽס������˵ijɼ��и������ȡһ������ijɼ����Ҹߵĸ��ʣ�
(2)��Ҫ����ѡ��һ�˲μӸ��������ͳ��ѧ�ĽǶȿ��ǣ�����Ϊѡ����λѧ���μӺ��ʣ�˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�������ij����Ʒ�����ǵ���ͬ�˿͵�ϲ�ã�����ͬʱ����A��B����Ʒ�ƣ�������������Ӫ�����ԣ���ϱ�����������������Ʒ�Ĵ�����ͳ�Ʒ�����AƷ�Ƶ���������y1��Ͷ���ʽ�x�����ȣ����ϵ��ͼ1��ʾ��BƷ�Ƶ���������y2��Ͷ���ʽ�x������ƽ���������ȣ����ϵ��ͼ2��ʾ���������ʽ�ĵ�λ����Ԫ���� 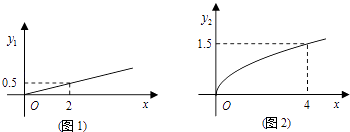
��1���ֱ�A��B����Ʒ�Ƶ���������y1��y2��ʾΪͶ���ʽ�x�ĺ�����ϵʽ��
��2�����̳��ƻ�Ͷ��5��Ԫ����������Ʒ����ȫ��Ͷ��A��B����Ʒ�ƣ��ʣ�����������5��Ԫ�ʽ𣬲���ʹ����������Ʒ�������������������Ϊ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}����an=2an-1-2n+5����n��N��n��2����a1=1��
��I����bn=an-2n+1����֤����{bn}��n��N*���dz����У�����{an}��ͨ�
��II����Sn������{an}��ǰn��ͣ���cn=��-1��nSn����{Cn}��ǰn���Tn��tn2��n��N*ʱ���������ʵ��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() sinxcosx��cos2x+
sinxcosx��cos2x+ ![]() ����x��R����
����x��R����
��1����������x��[�� ![]() ��
�� ![]() ]������f��x����a����a��ȡֵ��Χ��
]������f��x����a����a��ȡֵ��Χ��
��2�����Ƚ�y=f��x����ͼ����ÿ���������겻�䣬�������Ϊԭ����2����Ȼ��������ƽ�� ![]() ����λ�õ�����y=g��x����ͼ������y=g��x����
����λ�õ�����y=g��x����ͼ������y=g��x���� ![]() ������[��2�У�4��]�ڵ��������֮�ͣ�
������[��2�У�4��]�ڵ��������֮�ͣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com