
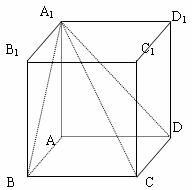
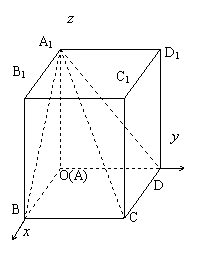
如图,长方体ABCD-A1B1C1D1的AA1=1,底面ABCD的周长为4。
⑴ 当长方体ABCD-A1B1C1D1的体积最大时,求二面角B-A1C-D的值;
⑵ 线段A1C上是否存在一点P,使得A1C 平面BPD,若有,求出P点的位置,没有请说明理由.
平面BPD,若有,求出P点的位置,没有请说明理由.
 .解:法一:
.解:法一:
⑴ 根据题意,长方体体积为
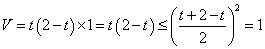 ……2分
……2分
当且仅当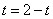 ,即
,即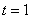 时体积
时体积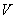 有最大值为1
有最大值为1
所以当长方体ABCD-A1B1C1D1的体积最大时,底面四边
形ABCD为正方形
作BM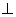 A1C于M,连接DM,BD
A1C于M,连接DM,BD
因为四边形ABCD为正方形,所以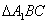 与
与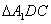 全等,故DM
全等,故DM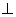 A1C,所以
A1C,所以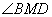 即为所求二面角的平面角 ……6分
即为所求二面角的平面角 ……6分
因为BC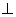 平面AA1B1B,所以
平面AA1B1B,所以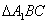 为直角三角形
为直角三角形
又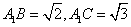 ,所以
,所以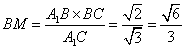 ,同理可得,
,同理可得,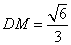
在 BMD中,根据余弦定理有:
BMD中,根据余弦定理有: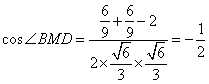
因为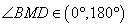 ,所以
,所以
即此时二面角B-A1C-D的值是 .
.
⑵ 若线段A1C上存在一点P,使得 A1C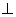 平面BPD,则A1C
平面BPD,则A1C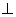 BD
BD
又A1A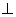 平面ABCD,所以A1A
平面ABCD,所以A1A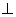 BD,所以BD
BD,所以BD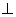 平面A1AC
平面A1AC
所以BD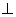 AC
AC
底面四边形ABCD为正方形,即只有ABCD为正方形时,线段A1C上存在点P满足要求,否则不存在
由⑴知,所求点P即为BM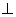 A1C的垂足M
A1C的垂足M
此时,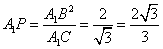 法二:
法二:
根据题意可知,AA1, AB,AD两两垂直,以AB为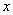 轴,AD为
轴,AD为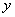 轴,AA1为
轴,AA1为 轴建立如图所示的空间直角坐标系:
轴建立如图所示的空间直角坐标系:
⑴长方体体积为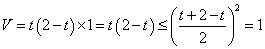 当且仅当
当且仅当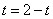 ,即
,即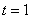 时体积
时体积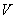 有最大值为1 所以当长方体ABCD-A1B1C1D1的体积最大时,底面四边形ABCD为正方形
有最大值为1 所以当长方体ABCD-A1B1C1D1的体积最大时,底面四边形ABCD为正方形
则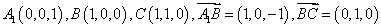 ,
,
设平面A1BC的法向量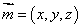 ,则
,则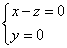
取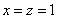 ,得:
,得: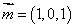
同理可得平面A1CD的法向量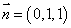
所以,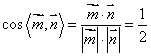
又二面角B-A1C-D为钝角,故值是 .
.
(也可以通过证明B1A 平面A1BC写出平面A1BC的法向量)
平面A1BC写出平面A1BC的法向量)
 |
⑵ 根据题意有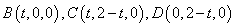 ,若线段A1C上存在一点P满足要求,不妨
,若线段A1C上存在一点P满足要求,不妨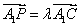 ,可得
,可得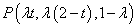
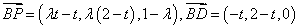
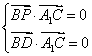 即:
即: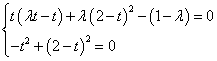
解得: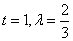
即只有当底面四边形是正方形时才有符合要求的点P,位置是线段A1C上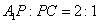 处.
处.


科目:高中数学 来源: 题型:
| |
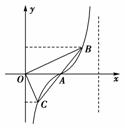
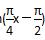 (0<x<4)的图象如图所示,A为图象与x轴的交点,过点A的直线l与函数的图象交于B、C两点,则(
(0<x<4)的图象如图所示,A为图象与x轴的交点,过点A的直线l与函数的图象交于B、C两点,则(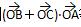 等于 ( )
等于 ( ) A.-8 B.-4 C.4 D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
将5名同学分到甲、乙、丙三个小组,若甲组至少两人,乙、丙两组每组至少一人,
则不同的分配方案种数
(A)80种 (B)120种 (C)140种 (D)50种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com