设等差数列{an}的公差d≠0,数列{bn}为等比数列,若a1=b1=a,a3=b3,a7=b5
(1)求数列{bn}的公比q;
(2)若an=bm,n,m∈N*,求n与m之间的关系;
(3)将数列{an},{bn}中的公共项按由小到大的顺序排列组成一个新的数列{cn},是否存在正整数p,q,r(p<q<r)使得p,q,r和cp+p,cq+q,cr+r均成等差数列?说明理由.
解:(1)设{b
n}的公比为q,由题意

即
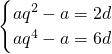
--------------------------------------------(2分)
q=1不合题意,故
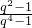
=

,解得q
2=2,
∴q=±

----------------(4分)
(2)由a
n=b
n得:a+(n-1)d=aq
n-1,又2d=aq
2-a=a,
∴d=

------------------(6分)
∴1+

=

即n+1=(±1)
m-1•
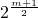
--------------------------(8分)
∵n+1∈N
*,
∴(±1)
m-1>0,
∴m为奇数,且n=
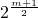
-1,-------(10分)
(3)若{a
n}与{b
n}有公共项,不妨设a
n=b
n,
由(2)知:m为奇数,且n=
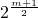
-1,
令m=2k-1(k∈N
*),则b
m=a•
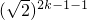
=a•2
k-1,
∴c
n=2
n-1a---------------------------------------------------------------(12分)
若存在正整数p、q、r(p<q<r)满足题意,则
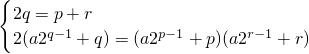
∴2
q=2
p-1+2
r-1,又2
p-1+2
r-1≥2
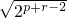
=

(当且仅当p=r时取“=”)
又∵p≠r,
∴2
p-1+2
r-1>

----------------------(14分)
又y=2
x在R上增,
∴q>
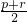
.与题设q=
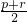
矛盾,
∴不存在p、q、r满足题意.---------------------------------------------------(16分)
分析:(1)依题意,通过解方程组

即可求得数列{b
n}的公比q;
(2)由a
n=b
n可求得d=

,代入整理有n+1=(±1)
m-1•
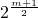
,可分析(±1)
m-1>0,从而可得n与m之间的关系;
(3)设a
n=b
n,令m=2k-1(k∈N
*),可求得b
m=a•2
k-1,令c
n=2
n-1a,若存在正整数p、q、r(p<q<r)满足题意
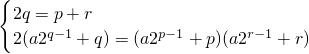
,由基本不等式可得出矛盾,从而可得结论.
点评:本题考查等差数列的通项公式与等比数列的通项公式的综合应用,考查方程思想与化归思想的综合运用,突出抽象思维与逻辑推理能力的考查,属于难题.

 即
即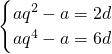 --------------------------------------------(2分)
--------------------------------------------(2分)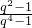 =
= ,解得q2=2,
,解得q2=2, ----------------(4分)
----------------(4分) ------------------(6分)
------------------(6分) =
= 即n+1=(±1)m-1•
即n+1=(±1)m-1•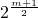 --------------------------(8分)
--------------------------(8分)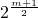 -1,-------(10分)
-1,-------(10分)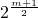 -1,
-1,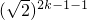 =a•2k-1,
=a•2k-1,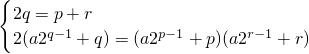
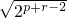 =
= (当且仅当p=r时取“=”)
(当且仅当p=r时取“=”) ----------------------(14分)
----------------------(14分)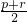 .与题设q=
.与题设q=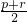 矛盾,
矛盾, 即可求得数列{bn}的公比q;
即可求得数列{bn}的公比q; ,代入整理有n+1=(±1)m-1•
,代入整理有n+1=(±1)m-1•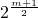 ,可分析(±1)m-1>0,从而可得n与m之间的关系;
,可分析(±1)m-1>0,从而可得n与m之间的关系;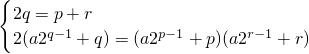 ,由基本不等式可得出矛盾,从而可得结论.
,由基本不等式可得出矛盾,从而可得结论.

 步步高达标卷系列答案
步步高达标卷系列答案