
实数的加法运算满足交换律a+b=b+a和结合律(a+b)+c=a+(b+c)。若对于正实数x和y定义![]() ,则( )
,则( )
A.”*”是可以交换的,但不可以结合 B.”*”是可以结合的,但不可以交换
C.”*”既不可以交换,也不可以结合 D.”*”是可以交换和结合的
科目:高中数学 来源: 题型:
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| T8 |
| T4 |
| T12 |
| T8 |
查看答案和解析>>
科目:高中数学 来源:2012届安徽省六校教育研究会高二素质测试理科数学 题型:选择题
实数的加法运算满足交换律a+b=b+a和结合律(a+b)+c=a+(b+c)。若对于正实数x和y定义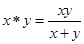 ,则(
)
,则(
)
A.”*”是可以交换的,但不可以结合 B.”*”是可以结合的,但不可以交换
C.”*”既不可以交换,也不可以结合 D.”*”是可以交换和结合的
查看答案和解析>>
科目:高中数学 来源:2010-2011学年安徽省六校教育研究会高二素质测试理科数学 题型:单选题
实数的加法运算满足交换律a+b=b+a和结合律(a+b)+c=a+(b+c)。若对于正实数x和y定义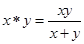 ,则( )
,则( )
| A.”*”是可以交换的,但不可以结合 | B.”*”是可以结合的,但不可以交换 |
| C.”*”既不可以交换,也不可以结合 | D.”*”是可以交换和结合的 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com