
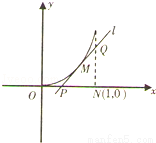
(2014•贵州模拟)函数f(x)=x2(0<x<1)的图象如图所示,其在点M(t,f(t))处的切线为l,l与x轴和直线x=1分别交与点P、Q,点N(1,0),若△PQN的面积为S时点M恰好有两个,则S的取值范围为( )
A.[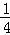 ,
,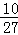 ) B.(
) B.( ,
,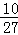 ] C.(
] C.(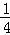 ,
,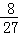 ) D.[
) D.[ ,
,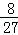 )
)
C
【解析】
试题分析:设M(t,t2),利用导数求出函数在M点处的切线方程,求出P,Q点的坐标,由三角形的面积公式求出△PQN的面积,由面积等于S整理,得到t3﹣4t2+4t=4S,令g(t)=t3﹣4t2+4t,由导数求出g(t)的最大值,再求出g(0),g(1)的值,从而得到△PQN的面积为S时点M恰好有两个时的4S的范围,则S的范围可求.
【解析】
设点M(t,t2),
由f(x)=x2(0<x<1),得:f′(x)=2x,
∴过点M的切线PQ的斜率k=2t.
∴切线PQ的方程为y=2tx﹣t2.
取y=0,得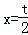 ,
,
取x=1,得y=2t﹣t2,
∴P(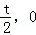 )、Q(1,2t﹣t2),
)、Q(1,2t﹣t2),
∴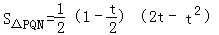 =S.
=S.
整理得:t3﹣4t2+4t﹣4S=0.
即t3﹣4t2+4t=4S.
令g(t)=t3﹣4t2+4t,
则g′(t)=3t2﹣8t+4,
由g′(t)=0,解得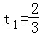 ,t2=2(舍).
,t2=2(舍).
∴当t∈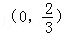 时,g′(t)>0,g(t)为增函数.
时,g′(t)>0,g(t)为增函数.
当t∈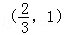 时,g′(t)<0,g(t)为减函数.
时,g′(t)<0,g(t)为减函数.
∴当t=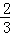 时,g(t)有极大值,也就是(0,1)上的最大值为
时,g(t)有极大值,也就是(0,1)上的最大值为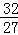 .
.
又g(0)=0,g(1)=1.
∴要使△PQN的面积为S时点M恰好有两个,
则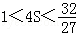 ,即
,即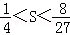 .
.
∴S的取值范围为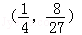 .
.
故选:C.


科目:高中数学 来源:[同步]2014年新人教B版选修4-5 2.2排序不等式练习卷(解析版) 题型:解答题
若a1≤a2≤…≤an,而b1≥b2≥…≥bn或a1≥a2≥…≥an而b1≤b2≤…≤bn,证明: ≤(
≤(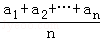 )•(
)•(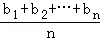 ).当且仅当a1=a2=…=an或b1=b2=…=bn时等号成立.
).当且仅当a1=a2=…=an或b1=b2=…=bn时等号成立.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 1.3绝对值不等式的解法练习卷(解析版) 题型:选择题
(2014•吉安二模)已知f(x)=|x﹣1|+|x+m|(m∈R),g(x)=2x﹣1,若m>﹣1,x∈[﹣m,1],不等式f(x)<g(x)恒成立,则实数m的取值范围是( )
A.(﹣1,﹣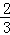 ] B.(﹣1,﹣
] B.(﹣1,﹣ ) C.(﹣∞,﹣
) C.(﹣∞,﹣ ] D.(﹣1,+∞)
] D.(﹣1,+∞)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修4-5 1.2基本不等式练习卷(解析版) 题型:选择题
(2014•湖南模拟)设点G是△ABC的重心,若∠A=120°,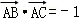 ,则
,则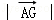 的最小值是( )
的最小值是( )
A.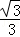 B.
B.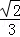 C.
C.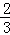 D.
D.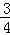
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修2-1 2.1曲线与方程练习卷(解析版) 题型:选择题
(2014•深圳二模)过点(0,﹣1)的直线l与两曲线y=lnx和x2=2py均相切,则p的值为( )
A. B.
B. C.2 D.4
C.2 D.4
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修2-1 2.1曲线与方程练习卷(解析版) 题型:选择题
(2014•吉林二模)已知曲线y=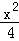 ﹣3lnx的一条切线的斜率为﹣
﹣3lnx的一条切线的斜率为﹣ ,则切点的横坐标为( )
,则切点的横坐标为( )
A.3 B.2 C.1 D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修2-1 2.1曲线与方程练习卷(解析版) 题型:选择题
(2014•锦州一模)函数y=lnx(x>0)的图象与直线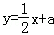 相切,则a等于( )
相切,则a等于( )
A.ln2﹣1 B.ln2+1 C.ln2 D.2ln2
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教B版选修1-2 4.2结构图练习卷(解析版) 题型:选择题
如图是一结构图,在 处应填入( )
处应填入( )
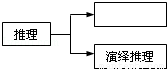
A.合情推理 B.三段论推理 C.类比推理 D.归纳推理
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-7 1.4分数法练习卷(解析版) 题型:填空题
(2012•湘潭三模)(优选法选做题)那霉素发酵液生物测定,一般都规定培养温度为(37±1)°C,培养时间在16小时以上,某制药厂为了缩短时间,决定优选培养温度,试验范围固定在32~45°C,精确度要求±1°C,用分数法安排实验,令第一试点在t1处,第二试点在t2处,则t1+t2= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com