
【题目】在平面直角坐标系xOy中,直线y=1与函数y=3sin ![]() x(0≤x≤10)的图象所有交点的横坐标之和为 .
x(0≤x≤10)的图象所有交点的横坐标之和为 .
【答案】30
【解析】解:∵y=3sin ![]() x的周期T=
x的周期T= ![]() =4,
=4,
∴当0≤x≤10时,其图象如下: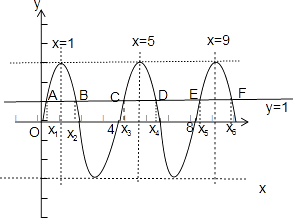
由图知,直线y=1与正弦曲线y=3sin ![]() x(0≤x≤10)相交于A、B、C、D、E、F6个点,其横坐标如图所示,
x(0≤x≤10)相交于A、B、C、D、E、F6个点,其横坐标如图所示,
则x1+x2=2,x3+x4=10,x5+x6=18,
∴所有交点的横坐标之和为2+10+18=30.
所以答案是:30.
【考点精析】解答此题的关键在于理解函数y=Asin(ωx+φ)的图象变换的相关知识,掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


科目:高中数学 来源: 题型:
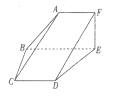
【题目】如图,平面![]() 平面
平面![]() 四边形
四边形![]() 为直角梯形,
为直角梯形, ![]() 四边形
四边形![]() 为等腰梯形,
为等腰梯形, ![]() 且
且![]()
(Ⅰ)若梯形![]() 内有一点
内有一点![]() ,使得
,使得![]() 平面
平面![]() ,求点
,求点![]() 的轨迹;
的轨迹;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() 为椭圆
为椭圆![]() 的左焦点,直线
的左焦点,直线![]() 被椭圆
被椭圆![]() 截得弦长为
截得弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)圆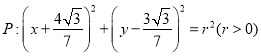 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点, ![]() 为线段
为线段![]() 上任意一点,直线
上任意一点,直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点
两点![]() 为圆
为圆![]() 的直径,且直线
的直径,且直线![]() 的斜率大于
的斜率大于![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中新网2016年12月19日电根据预报,今天开始雾霾范围将进一步扩大, ![]() 日夜间至
日夜间至![]() 日,雾霾严重时段部分地区
日,雾霾严重时段部分地区![]() 浓度峰值会超过
浓度峰值会超过![]() 微克/立方米. 而此轮雾霾最严重的时段,将有包括京津冀、山西、陕西、河南等
微克/立方米. 而此轮雾霾最严重的时段,将有包括京津冀、山西、陕西、河南等![]() 个省市在内的地区被雾霾笼罩.
个省市在内的地区被雾霾笼罩. ![]() 是指大气中直径小于或等于
是指大气中直径小于或等于![]() 微米的顆粒物,也称为可人肺颗粒物.
微米的顆粒物,也称为可人肺颗粒物. ![]() 日均值在
日均值在![]() 微克/立方米以下空气质量为一级;在
微克/立方米以下空气质量为一级;在![]() 微克/立方米
微克/立方米![]() 微克/立方米之间空气质量为二级;在
微克/立方米之间空气质量为二级;在![]() 微克/立方米以上空气质量为超标.某地区在2016年12月19日至28日每天的
微克/立方米以上空气质量为超标.某地区在2016年12月19日至28日每天的![]() 监测数据的茎叶图如下:
监测数据的茎叶图如下:

(1)求出这些数据的中位数与极差;
(2)从所给的空气质量不超标的![]() 天的数据中任意抽取
天的数据中任意抽取![]() 天的数据,求这
天的数据,求这![]() 天中恰好有
天中恰好有![]() 天空气质量为一级,另一天空气质量为二级的概率.
天空气质量为一级,另一天空气质量为二级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈A,且A={x|a﹣1<x<a+1},命题q:x∈B,且B={x|x2﹣4x+3≥0}
(Ⅰ)若A∩B=,A∪B=R,求实数a的值;
(Ⅱ)若p是q的充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个命题:
①若 ![]() <
< ![]() <0,则
<0,则 ![]() +
+ ![]() >2;
>2;
②若a>b,则am2>bm2;
③在△ABC中,若sinA=sinB,则A=B;
④任意x∈R,都有ax2﹣ax+1≥0,则0<a≤4.
其中是真命题的有( )
A.①②
B.②③
C.①③
D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某条公共汽车线路收支差额![]() 与乘客量
与乘客量![]() 的函数关系如图所示(收支差额
的函数关系如图所示(收支差额![]() 车票收入
车票收入![]() 支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变车票价格,减少支出费用;建议(Ⅱ)不改变支出费用,提高车票价格,下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则
支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变车票价格,减少支出费用;建议(Ⅱ)不改变支出费用,提高车票价格,下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则
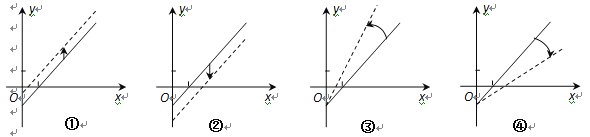
A. ①反映了建议(Ⅱ),③反映了建议(Ⅰ)
B. ①反映了建议(Ⅰ),③反映了建议(Ⅱ)
C. ②反映了建议(Ⅰ),④反映了建议(Ⅱ)
D. ④反映了建议(Ⅰ),②反映了建议(Ⅱ)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市统计局就某地居民的月收入调查了10 000人,并根据所得数据画出样本的频率分布直方图如图所示.(每个分组包括左端点,不包括右端点,如第一组表示[1 000,1 500)。

(1)求居民收入在[2000,3 000)的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10 000人中按分层抽样方法抽出100人作进一步分析,则月收入在[2 000,3 000)的这段应抽取多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com