
【题目】某市统计局就某地居民的月收入调查了10 000人,并根据所得数据画出样本的频率分布直方图如图所示.(每个分组包括左端点,不包括右端点,如第一组表示[1 000,1 500)。

(1)求居民收入在[2000,3 000)的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10 000人中按分层抽样方法抽出100人作进一步分析,则月收入在[2 000,3 000)的这段应抽取多少人?
【答案】(1)0.5 (2)2400 (3)25
【解析】
试题分析:(1)根据频率=小矩形的高×组距来求;(2)根据中位数的左右两边的矩形的面积和相等,所以只需求出从左开始面积和等于0.5的底边横坐标的值即可,运用取中间数乘频率,再求之和,计算可得平均数;(3)求出月收入在[2000,3000)的人数,用分层抽样的抽取比例乘以人数,可得答案
试题解析:(Ⅰ)月收入在[3000,3500)的频率为
0.0005×(3000-2000)=0.5
(Ⅱ)∵0.0002×(1500-1000)=0.1,
0.0004×(2000-1500)=0.2,
0.0005×(2500-2000)=0.25
0.1+0.2+0.25=0.55>0.5
所以,样本数据的中位数为
2000+![]() =2000+400=2400(元)
=2000+400=2400(元)
(Ⅲ)居民月收入在[2500,3000)的频数为0.25×10000=2500(人),
再从10000人中用分层抽样方法抽出100人,则月收入在[2500,3000)的这段应抽取100×![]() =25(人)
=25(人)


科目:高中数学 来源: 题型:
【题目】某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:

其中一个数字被污损.
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率.
(2)随着节目的播出,极大激发了观众对成语知识的学习积累的热情,从中获益匪浅.现从观看该节目的观众中随机统计了4位观众的周均学习成语知识的时间![]() (单位:小时)与年龄
(单位:小时)与年龄![]() (单位:岁),并制作了对照表(如下表所示)
(单位:岁),并制作了对照表(如下表所示)
年龄 | 20 | 30 | 40 | 50 |
周均学习成语知识时间 | 2.5 | 3 | 4 | 4.5 |
由表中数据,试求线性回归方程![]() ,并预测年龄为55岁观众周均学习成语知识时间.
,并预测年龄为55岁观众周均学习成语知识时间.
参考公式: 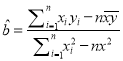 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
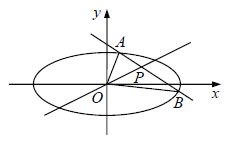
【题目】已知点![]() 在椭圆
在椭圆![]() 内,过
内,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于A,B两点,且点
相交于A,B两点,且点![]() 是线段AB的中点,O为坐标原点.
是线段AB的中点,O为坐标原点.
(Ⅰ)是否存在实数t,使直线![]() 和直线OP的倾斜角互补?若存在,求出
和直线OP的倾斜角互补?若存在,求出![]() 的值,若不存在,试说明理由;
的值,若不存在,试说明理由;
(Ⅱ)求![]() 面积S的最大值.
面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:


将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成上面的![]() 列联表,若按
列联表,若按![]() 的可靠性要求,并据此资料,你是否认为“体育迷”与性别有关?
的可靠性要求,并据此资料,你是否认为“体育迷”与性别有关?
(2)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为![]() .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求![]() 分布列,期望
分布列,期望![]() 和方差
和方差![]() .
.
附: 

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, ![]() 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若![]() 时从区间
时从区间![]() 上任取的一个数,
上任取的一个数, ![]() 是从区间
是从区间![]() 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】.(本小题满分12分)
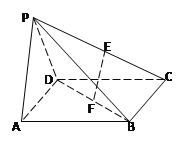
如图,四棱锥P—ABCD中,底面ABCD是边长为![]() 的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=![]() AD.
AD.
(Ⅰ)求证:EF//平面PAD;
(Ⅱ)求三棱锥C—PBD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com