
已知函数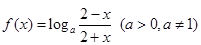 .
.
(Ⅰ)当a=3时,求函数 在
在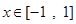 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)求函数 的定义域,并求函数
的定义域,并求函数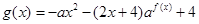 的值域。(用a表示)
的值域。(用a表示)
(Ⅰ)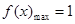 ,
,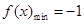 ;(Ⅱ)
;(Ⅱ)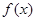 的定义域为
的定义域为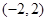 ,
,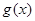 的值域为
的值域为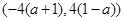 .
.
【解析】
试题分析:(Ⅰ)当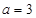 时,求函数
时,求函数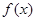 在
在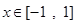 上的最大值和最小值,令
上的最大值和最小值,令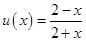 ,变形得到该函数的单调性,求出其值域,再由
,变形得到该函数的单调性,求出其值域,再由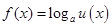 为增函数,从而求得函数
为增函数,从而求得函数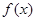 在
在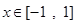 上的最大值和最小值;(Ⅱ)求函数
上的最大值和最小值;(Ⅱ)求函数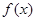 的定义域,由对数函数的真数大于0求出函数
的定义域,由对数函数的真数大于0求出函数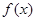 的定义域,求函数
的定义域,求函数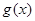 的值域,函数
的值域,函数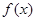 的定义域,即
的定义域,即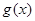 的定义域,把
的定义域,把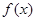 的解析式代入
的解析式代入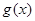 后整理,化为关于
后整理,化为关于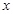 的二次函数,对
的二次函数,对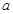 分类讨论,由二次函数的单调性求最值,从而得函数
分类讨论,由二次函数的单调性求最值,从而得函数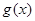 的值域.
的值域.
试题解析:(Ⅰ)令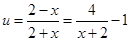 ,显然
,显然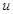 在
在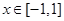 上单调递减,故
上单调递减,故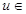
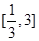 ,
,
故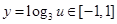 ,即当
,即当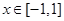 时,
时,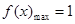 ,(在
,(在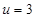 即
即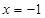 时取得)
时取得)
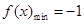 ,(在
,(在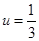 即
即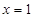 时取得)
时取得)
(II)由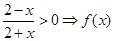 的定义域为
的定义域为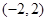 ,由题易得:
,由题易得: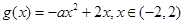 ,
,
因为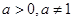 ,故
,故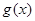 的开口向下,且对称轴
的开口向下,且对称轴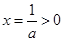 ,于是:
,于是:
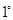 当
当 即
即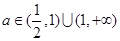 时,
时,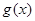 的值域为(
的值域为(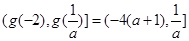 ;
;
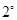 当
当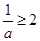 即
即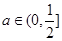 时,
时,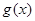 的值域为(
的值域为(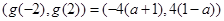
考点:复合函数的单调性;函数的值域.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com