
已知函数f(x)=-x3+ax2+bx+c在(-∞,0)上是减函数,在(0,1)上是增函数,函数f(x)在R上有三个零点,且1是其中一个零点.
(1)求b的值 (2)求f(2)的取值范围
(1)0 (2)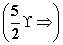
【解析】 (1)∵f(x)=-x3+ax2+bx+c,
∴f ′(x)=-3x2+2ax+b. …………3分
∵f(x)在(-∞,0)上是减函数,在(0,1)上是增函数,
∴当x=0时,f(x)取到极小值,即f ′(0)=0,
∴b=0.
(2)由(1)知,f(x)=-x3+ax2+c,
∵1是函数f(x)的一个零点,即f(1)=0,∴c=1-a.
∵f′(x)=-3x2+2ax=0的两个根分别为x1=0,x2=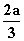 .
.
又∵f(x)在(-∞,0)上是减函数,在(0,1)上是增函数,且函数f(x)在R上有三个零点,
∴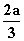 应是f(x)的一个极大值点,因此应有x2=
应是f(x)的一个极大值点,因此应有x2=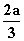 >1,即a>
>1,即a>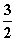 .
.
∴f(2)=-8+4a+(1-a)=3a-7>-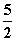 .
.
故f(2)的取值范围为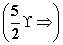 .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
有下列四个命题:
①“若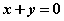 , 则
, 则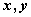 互为相反数”的逆命题;
互为相反数”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若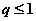 ,则
,则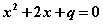 有实根”的逆否命题;
有实根”的逆否命题;
④“存在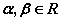 ,使
,使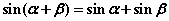 成立”的否定.
成立”的否定.
其中真命题为 ( )
A.①② B.②③ C.①③ D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
下列命题中真命题的个数为:( )
①命题“若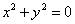 ,则x,y全为0”的逆命题;
,则x,y全为0”的逆命题;
②命题“全等三角形是相似三角形”的否命题;
③命题“若m>0,则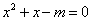 有实根”的逆否命题;
有实根”的逆否命题;
④命题“在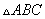 中,
中, 、
、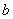 、
、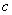 分别是角A、B、C所对的边长,若
分别是角A、B、C所对的边长,若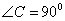 ,则
,则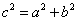 ”的逆否命题。
”的逆否命题。
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com