
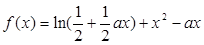
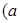 为常数,
为常数,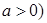
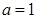 时,求函数
时,求函数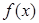 在
在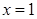 处的切线方程;
处的切线方程; 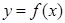 在
在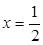 处取得极值时,若关于
处取得极值时,若关于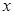 的方程
的方程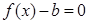 在
在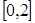 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;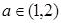 ,总存在
,总存在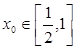 ,使不等式
,使不等式 成立,求实数
成立,求实数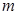 的取值范围。
的取值范围。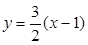 (2)
(2) 
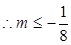
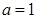 时,
时,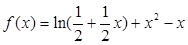
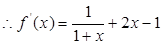 ,于是
,于是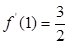 ,又
,又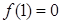 ,即切点为(
,即切点为(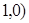
 切线方程为
切线方程为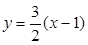 —————————————————————————5分
—————————————————————————5分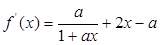 ,
,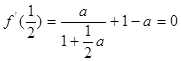 ,即
,即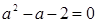 ,
,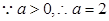
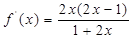 ,
,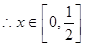 上减,
上减,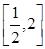 上增,
上增,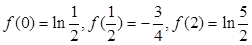
 ———————————————————————————10分
———————————————————————————10分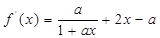
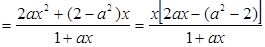
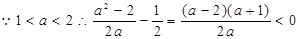 ,即
,即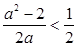 (
(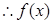 在
在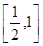 上增,
上增,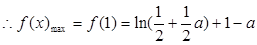
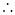 只须
只须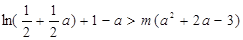 ————————————————12分
————————————————12分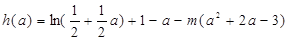
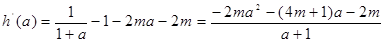
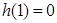
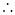
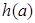 在1的右侧需先增,
在1的右侧需先增,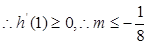
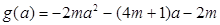 ,对称轴
,对称轴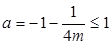
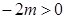 ,
,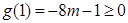
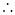 在
在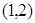 上,
上,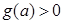 ,即
,即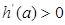
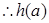 在
在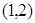 上单调递增,
上单调递增,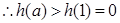
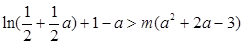 ,
,
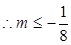 ——————————————————-15分
——————————————————-15分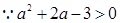
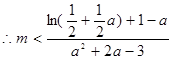
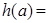
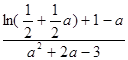 ,
,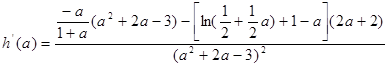
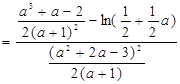
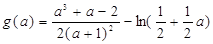 ,
,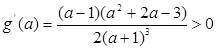
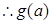 在
在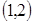 上增,又
上增,又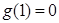 ,
,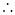
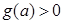 ,即
,即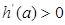 ,
,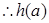 在
在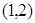 上增
上增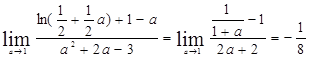
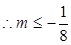
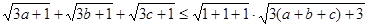
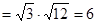 ——————————————————5分
——————————————————5分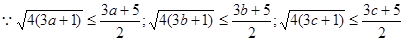

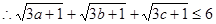 ——————————————————————5分
——————————————————————5分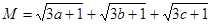
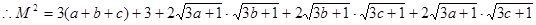
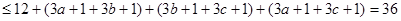
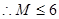 —————————————————————————————————5分
—————————————————————————————————5分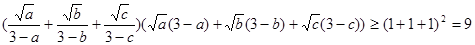
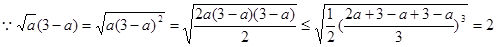
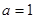 时取“=”号;同理:
时取“=”号;同理: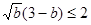 ,
,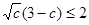 .
.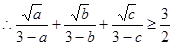 ,所以,当
,所以,当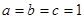 时,
时,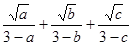 的最小值为
的最小值为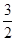
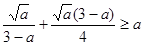 ,其中
,其中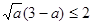 也可以构造函数
也可以构造函数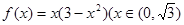 用导数求最大值)—————————10分
用导数求最大值)—————————10分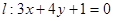
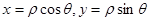 代入直线方程得:
代入直线方程得: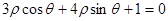
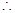 直线
直线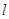 的极坐标方程为:
的极坐标方程为: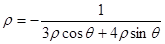 .————————————3分
.————————————3分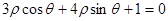 的形式不扣分)
的形式不扣分)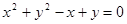 ————————————4分
————————————4分 ——————————————5分
——————————————5分 ,
,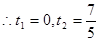 ;
;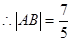 ———————————7分
———————————7分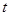 ,则
,则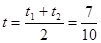 ,
,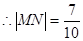 —————————————————————————————10分
—————————————————————————————10分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com