
某商场准备在五一劳动节期间举行促销活动,根据市场调查,该商场决定从3种服装商品、2种家电商品、4种日用商品中,选出3种商品进行促销活动.
(Ⅰ)试求选出的3种商品中至少有一种日用商品的概率;
(Ⅱ)商场对选出的A商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高90元,同时允许顾客有3次抽奖的机会,若中奖,则每次中奖都可获得一定数额的奖金.假设顾客每次抽奖时获奖与否是等可能的,请问:商场应将中奖奖金数额最高定为多少元,才能使促销方案对自己有利?
(Ⅰ)P=1-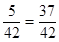 .
.
(Ⅱ)要使促销方案对商场有利,应使顾客获奖奖金数的期望值不大于商场的提价数额,因此应有1.5x≤90,所以x≤60,故商场应将中奖奖金数额最高定为60元,才能使促销方案对自己有利.
解析试题分析:(Ⅰ)从3种服装商品、2种家电商品、4种日用商品中,选出3种商品,一共可以有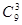 种不同的选法. 选出的3种商品中,没有日用商品的选法有
种不同的选法. 选出的3种商品中,没有日用商品的选法有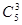 种,所以选出的3种商品中至少有一种日用商品的概率为P=1-
种,所以选出的3种商品中至少有一种日用商品的概率为P=1-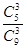 =1-
=1-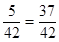 .
.
(Ⅱ)假设商场将中奖奖金数额定为x元,则顾客在三次抽奖中所获得的奖金总额是一随机变量ξ,其所有可能的取值为,0,x,2x,3x.
ξ=0时表示顾客在三次抽奖中都没有获奖,所以P(ξ=0)=(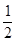 )3=
)3= ,
,
同理可得P(ξ=x)=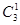 (
(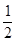 )(
)(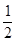 )2=
)2=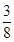 ,
,
P(ξ=2x)= (
(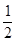 )2(
)2(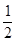 )=
)=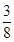 ,P(ξ=3x)=(
,P(ξ=3x)=(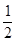 )3=
)3= .
.
于是顾客在三次抽奖中所获得的奖金总额的期望是
Eξ=0× +x·
+x·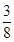 +2x·
+2x·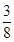 +3x·
+3x· =1.5x.
=1.5x.
要使促销方案对商场有利,应使顾客获奖奖金数的期望值不大于商场的提价数额,因此应有1.5x≤90,所以x≤60,故商场应将中奖奖金数额最高定为60元,才能使促销方案对自己有利.
考点:古典概型概率的计算,互斥(对立)事件的概率计算,数学期望的应用。
点评:中档题,本题综合性较强,综合考查古典概型概率的计算,互斥(对立)事件的概率计算,数学期望的应用,及利用数学知识解决实际问题的能力。求出顾客在三次抽奖中所获得的奖金总额的期望值,与商场的提价数额比较,即可求得结论。


科目:高中数学 来源: 题型:解答题
设 是定义在
是定义在 的可导函数,且不恒为0,记
的可导函数,且不恒为0,记 .若对定义域内的每一个
.若对定义域内的每一个 ,总有
,总有 ,则称
,则称 为“
为“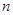 阶负函数 ”;若对定义域内的每一个
阶负函数 ”;若对定义域内的每一个 ,总有
,总有 ,则称
,则称 为“
为“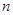 阶不减函数”(
阶不减函数”( 为函数
为函数 的导函数).
的导函数).
(1)若 既是“1阶负函数”,又是“1阶不减函数”,求实数
既是“1阶负函数”,又是“1阶不减函数”,求实数 的取值范围;
的取值范围;
(2)对任给的“2阶不减函数” ,如果存在常数
,如果存在常数 ,使得
,使得 恒成立,试判断
恒成立,试判断 是否为“2阶负函数”?并说明理由.
是否为“2阶负函数”?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,要用栏杆围成一个面积为50平方米的长方形花园,其中有一面靠墙不需要栏杆,其中正面栏杆造价每米200元,两个侧面栏杆每米造价50元,设正面栏杆长度为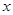 米.
米.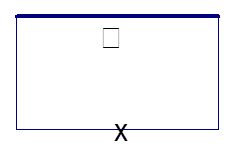
(1)将总造价y表示为关于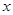 的函数;
的函数;
(2)问花园如何设计,总造价最少?并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂生产一种仪器的元件,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知道,其次品率P与日产量x(万件)之间大体满足关系: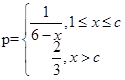 (其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器的元件每天的盈利额T(万元)表示为日产量x(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有一批货物需要用汽车从生产商所在城市甲运至销售商所在城市乙,已知从城市甲到城市乙只有两条公路,且通过这两条公路所用的时间互不影响。
据调查统计,通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数分布如下表:
| 所用的时间(天数) | 10 | 11 | 12 | 13 |
| 通过公路1的频数 | 20 | 40 | 20 | 20 |
| 通过公路2的频数 | 10 | 40 | 40 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂生产一种仪器,由于受生产能力和技术水平的限制,会产生一些次品,根据以往的经验知道,其次品率P与日产量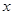 (件)之间近似满足关系:
(件)之间近似满足关系: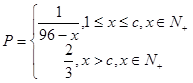 (其中
(其中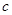 为小于96的正整常数)
为小于96的正整常数)
(注:次品率P= ,如P=0.1表示每生产10件产品,有1件次品,其余为合格品.)已知每生产一件合格的仪器可以盈利A元,但每生产一件次品将亏损A/2元,故厂方希望定出合适的日产量。
,如P=0.1表示每生产10件产品,有1件次品,其余为合格品.)已知每生产一件合格的仪器可以盈利A元,但每生产一件次品将亏损A/2元,故厂方希望定出合适的日产量。
试将生产这种仪器每天的赢利T(元)表示为日产量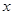 (件的函数);
(件的函数);
当日产量为多少时,可获得最大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com