
【题目】已知函数![]() (
(![]() ).
).
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数
垂直,求函数![]() 的单调区间;
的单调区间;
(2)若对于任意![]() ,都有
,都有![]() 成立,试求a的取值范围.
成立,试求a的取值范围.
科目:高中数学 来源: 题型:
【题目】随着网络和智能手机的普及与快速发展,许多可以解答各学科问题的搜题软件走红.有教育工作者认为:网搜答案可以起到拓展思路的作用,但是对多数学生来讲,容易产生依赖心理,对学习能力造成损害.为了了解网络搜题在学生中的使用情况,某校对学生在一周时间内进行网络搜题的频数进行了问卷调查,并从参与调查的学生中抽取了男、女学生各50人进行抽样分析,得到如下样本频数分布表:
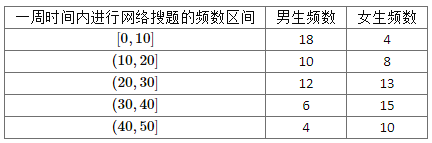
将学生在一周时间内进行网络搜题频数超过20次的行为视为“经常使用网络搜题”,不超过20次的视为“偶尔或不用网络搜题”.
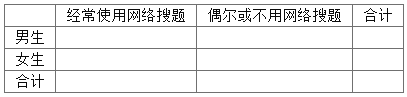
(1)根据已有数据,完成下列![]() 列联表(单位:人)中数据的填写,并判断是否在犯错误的概率不超过1%的前提下有把握认为使用网络搜题与性别有关?
列联表(单位:人)中数据的填写,并判断是否在犯错误的概率不超过1%的前提下有把握认为使用网络搜题与性别有关?
(2)将上述调查所得到的频率视为概率,从该校所有参与调查的学生中,采用随机抽样的方法每次抽取一个人,抽取4人,记经常使用网络搜题的人数为![]() ,若每次抽取的结果是相互独立的,求随机变量
,若每次抽取的结果是相互独立的,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《朗读者》是一档文化情感类节目,以个人成长、情感体验、背景故事与传世佳作相结合的方式,选用精美的文字,用最平实的情感读出文字背后的价值,深受人们的喜爱.为了了解人们对该节目的喜爱程度,某调查机构随机调查了![]() ,
,![]() 两个城市各100名观众,得到下面的列联表.
两个城市各100名观众,得到下面的列联表.
非常喜爱 | 喜爱 | 合计 | |
| 60 | 100 | |
| 30 | ||
合计 | 200 |
完成上表,并根据以上数据,判断是否有![]() 的把握认为观众的喜爱程度与所处的城市有关?
的把握认为观众的喜爱程度与所处的城市有关?
附参考公式和数据: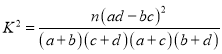 (其中
(其中![]() ).
).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司在某市的货物转运中心,拟引进智能机器人分拣系统,以提高分拣效率和降低物流成本,已知购买x台机器人的总成本p(x)=![]() 万元.
万元.
(1)若使每台机器人的平均成本最低,问应买多少台?
(2)现按(1)中的数量购买机器人,需要安排m人将邮件放在机器人上,机器人将邮件送达指定落袋格口完成分拣,经实验知,每台机器人的日平均分拣量q(m)=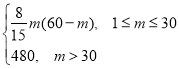 (单位:件),已知传统人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大值时,用人数量比引进机器人前的用人数量最多可减少百分之几?
(单位:件),已知传统人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大值时,用人数量比引进机器人前的用人数量最多可减少百分之几?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 是自然对数的底数,
是自然对数的底数,![]() .
.
(1) 若![]() 是函数
是函数![]() 的导函数,当
的导函数,当![]() 时,解关于
时,解关于![]() 的不等式
的不等式![]() ;
;
(2) 若![]() 在
在![]() 上是单调增函数,求
上是单调增函数,求![]() 的取值范围;
的取值范围;
(3) 当![]() 时,求整数
时,求整数![]() 的所有值,使方程
的所有值,使方程![]() 在
在![]() 上有解.
上有解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ax2+bx+c(a≠0),满足条件f(x+1)-f(x)=2x(x∈R),且f(0)=1.
(Ⅰ)求f(x)的解析式;
(Ⅱ)当x≥0时,f(x)≥mx-3恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过椭圆E:![]() 1(a>b>0)上一动点P向圆O:x2+y2=b2引两条切线PA,PB,切点分别是A,B.直线AB分别与x轴,y轴交于点M,N(O为坐标原点).
1(a>b>0)上一动点P向圆O:x2+y2=b2引两条切线PA,PB,切点分别是A,B.直线AB分别与x轴,y轴交于点M,N(O为坐标原点).

(1)若在椭圆E上存在点P,满足PA⊥PB,求椭圆E的离心率的取值范围;
(2)求证:在椭圆E内,存在一点C满足|CO|=|CA|=|CP|=|CB|;
(3)若椭圆E的短轴长为2,△MON面积的最小值为![]() ,求椭圆E的方程.
,求椭圆E的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com