
分析 利用“切化弦”的思想,把左边化成等于右边即可.
解答 证明:由$\frac{{{{cos}^2}α-{{sin}^2}α}}{1-2sinαcosα}$=$\frac{(cosα-sinα)(cosα+sinα)}{co{s}^{2}α+si{n}^{2}α-2sinαcosα}$=$\frac{cosα+sinα}{cosα-sinα}$=$\frac{\frac{cosα+sinα}{cosα}}{\frac{cosα-sinα}{cosα}}=\frac{1+tanα}{1-tanα}$
左边=右边.
得证
点评 本题考查了“切化弦”或“弦化切”的思想,灵活运用同角三角函数关系式是化简此题的关键.属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 有99%的人认为该栏目优秀 | |
| B. | 有99%的人认为栏目是否优秀与改革有关 | |
| C. | 有99%的把握认为电视栏目是否优秀与改革有关系 | |
| D. | 以上说法都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 该函数的值域是[-1,1] | |
| B. | 当且仅当2kπ+π<x<2kπ+$\frac{3π}{2}$(k∈Z)时,f(x)<0 | |
| C. | 当且仅当x=2kπ+$\frac{π}{2}$(k∈Z)时,该函数取得最大值 | |
| D. | 该函数是以π为最小正周期的周期函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
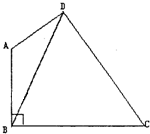 如图:在一座山上要打一个涵洞,在山周围取四个点A、B、C、D,使AB⊥BC,又测得∠DAB=120°,DA=3km,DC=7km,BC=3$\sqrt{3}$km,求:涵洞DB的长.
如图:在一座山上要打一个涵洞,在山周围取四个点A、B、C、D,使AB⊥BC,又测得∠DAB=120°,DA=3km,DC=7km,BC=3$\sqrt{3}$km,求:涵洞DB的长.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=0 | B. | f(x)=2x+$\frac{1}{2^x}$ | C. | f(x)=sinx+x | D. | f(x)=lg|x|+x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com