
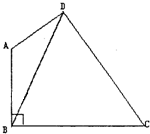
 如图:在一座山上要打一个涵洞,在山周围取四个点A、B、C、D,使AB⊥BC,又测得∠DAB=120°,DA=3km,DC=7km,BC=3$\sqrt{3}$km,求:涵洞DB的长.
如图:在一座山上要打一个涵洞,在山周围取四个点A、B、C、D,使AB⊥BC,又测得∠DAB=120°,DA=3km,DC=7km,BC=3$\sqrt{3}$km,求:涵洞DB的长. 分析 △ABD中,由正弦定理求得 sinα=$\frac{3\sqrt{3}}{2x}$.△BCD中,由余弦定理求得sinα=$\frac{{x}^{2}+27-49}{2x•3\sqrt{3}}$=$\frac{{x}^{2}-22}{6\sqrt{3}x}$,由$\frac{3\sqrt{3}}{2x}$=$\frac{{x}^{2}-22}{6\sqrt{3}x}$,求得涵洞BD=x的长.
解答 解:∵∠DAB=120°,DA=3km,DC=7km,BC=3$\sqrt{3}$km,设BD=xkm,∠ABD=α,
△ABD中,由正弦定理得$\frac{3}{sinα}$=$\frac{x}{sin120°}$,∴sinα=$\frac{3\sqrt{3}}{2x}$.
△BCD中,由余弦定理得cos∠DBC=cos($\frac{π}{2}$-α)=sinα=$\frac{{x}^{2}+27-49}{2x•3\sqrt{3}}$=$\frac{{x}^{2}-22}{6\sqrt{3}x}$,
由$\frac{3\sqrt{3}}{2x}$=$\frac{{x}^{2}-22}{6\sqrt{3}x}$,求得x=7km,故涵洞BD的长为7km.
点评 本题主要考查解三角形的实际应用,正弦定理和余弦定理,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
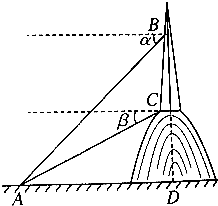 在山顶铁塔上B处测得地面上一点A的俯角α=54°40′,在塔底C处测得A处的俯角β=50°1′.已知铁塔BC部分的高为27.3m,求出山高CD(精确到1m).
在山顶铁塔上B处测得地面上一点A的俯角α=54°40′,在塔底C处测得A处的俯角β=50°1′.已知铁塔BC部分的高为27.3m,求出山高CD(精确到1m).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<1} | B. | {x|0≤x<1} | C. | {x|-3<x<2} | D. | {x|-3<x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com