
分析 联立直线和圆的方程,求得交点A,B的坐标,然后利用数量积的坐标运算得答案.
解答 解:如图,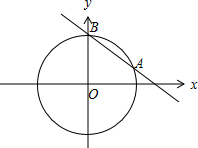
联立$\left\{\begin{array}{l}{x+\sqrt{3}y-2\sqrt{3}=0}\\{{x}^{2}+{y}^{2}=4}\end{array}\right.$,解得A($\sqrt{3},1$),B(0,2),
∴$\overrightarrow{OA}•\overrightarrow{OB}$=($\sqrt{3},1$)•(0,2)=$\sqrt{3}×0+1×2=2$.
故答案为:2.
点评 本题考查数量积的坐标运算,考查了直线和圆的位置关系,是中档题.


科目:高中数学 来源: 题型:解答题
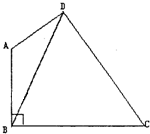 如图:在一座山上要打一个涵洞,在山周围取四个点A、B、C、D,使AB⊥BC,又测得∠DAB=120°,DA=3km,DC=7km,BC=3$\sqrt{3}$km,求:涵洞DB的长.
如图:在一座山上要打一个涵洞,在山周围取四个点A、B、C、D,使AB⊥BC,又测得∠DAB=120°,DA=3km,DC=7km,BC=3$\sqrt{3}$km,求:涵洞DB的长.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=0 | B. | f(x)=2x+$\frac{1}{2^x}$ | C. | f(x)=sinx+x | D. | f(x)=lg|x|+x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}+\frac{3}{2}$i | B. | -$\frac{1}{2}-\frac{3}{2}$i | C. | -$\frac{1}{2}-\frac{1}{2}$i | D. | $\frac{1}{2}+\frac{1}{2}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 6 | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
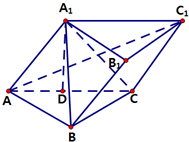 在斜三棱柱ABC-A1B1C1中BC⊥CC1,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D.
在斜三棱柱ABC-A1B1C1中BC⊥CC1,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com