
分析 根据条件及余弦定理即可求出c2=64,进而得出c=8,再根据余弦定理可求出cosB=$\frac{1}{2}$,这样根据向量投影的计算公式即可求出$\overrightarrow{AB}$在$\overrightarrow{BC}$方向上的投影.
解答 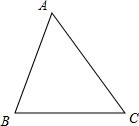 解:如图,△ABC中,$a=5,b=7,cosC=\frac{1}{7}$;
解:如图,△ABC中,$a=5,b=7,cosC=\frac{1}{7}$;
∴由余弦定理得,c2=a2+b2-2abcosC=25+49-10=64;
∴c=8;
∴$cosB=\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}=\frac{25+64-49}{80}=\frac{1}{2}$;
∴$\overrightarrow{AB}$在$\overrightarrow{BC}$方向上的投影为$|\overrightarrow{AB}|•cos<\overrightarrow{AB},\overrightarrow{BC}>=|\overrightarrow{AB}|•(-cosB)$=$8×(-\frac{1}{2})=-4$.
故答案为:-4.
点评 考查余弦定理,向量夹角的定义,三角函数的诱导公式,以及一个向量在另一个向量方向上的投影的定义及计算公式.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{13}$ | B. | $\frac{{\sqrt{13}}}{5}$ | C. | $\sqrt{65}$ | D. | $\frac{{\sqrt{65}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
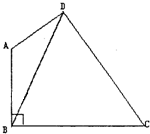 如图:在一座山上要打一个涵洞,在山周围取四个点A、B、C、D,使AB⊥BC,又测得∠DAB=120°,DA=3km,DC=7km,BC=3$\sqrt{3}$km,求:涵洞DB的长.
如图:在一座山上要打一个涵洞,在山周围取四个点A、B、C、D,使AB⊥BC,又测得∠DAB=120°,DA=3km,DC=7km,BC=3$\sqrt{3}$km,求:涵洞DB的长.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}+\frac{3}{2}$i | B. | -$\frac{1}{2}-\frac{3}{2}$i | C. | -$\frac{1}{2}-\frac{1}{2}$i | D. | $\frac{1}{2}+\frac{1}{2}i$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com