
已知抛物线y=x2﹣1上的一定点B(﹣1,0)和两个动点PQ、,当BP⊥PQ时,点Q的横坐标的取值范围是( )
A. (﹣∞,﹣3]∪[1,+∞) B. [﹣3,1]
C. (﹣∞,﹣3]∪[1,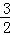 )∪(
)∪(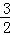 ,+∞) D. [1,+∞)
,+∞) D. [1,+∞)
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD.将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图15所示.
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
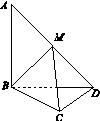
图15
查看答案和解析>>
科目:高中数学 来源: 题型:
有两张卡片,一张的正反面分别写着数字0与1,另一张的正反面分别写着数字2与3,将两张卡片排在一起组成一个两位数,则所组成的两位数为奇数的概率是( )
A.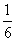 B.
B.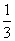
C.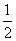 D.
D.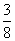
查看答案和解析>>
科目:高中数学 来源: 题型:
.一位客人游览福州鼓山、福州永泰天门山、福州青云山这三个景点的概率分别是0.4,0.5,0.6,且客人是否游览哪个景点互不影响,设Y表示客人离开福州市时游览的景点数与没有游览的景点数之差的绝对值.求Y的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知某空间几何体的正视图和侧视图相同,且如图所示,俯视图是两个同心圆,则它的表面积为( )
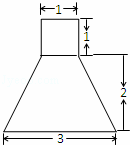
A. 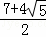 π B. (12+4
π B. (12+4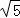 )π C.
)π C. 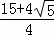 π D. (13+4
π D. (13+4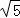 )π
)π
查看答案和解析>>
科目:高中数学 来源: 题型:
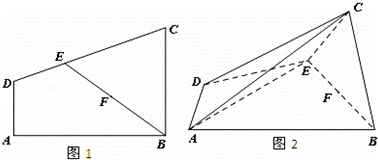
如图1,在直角梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,E为CD上一点,且DE=1,EC=2,现沿BE折叠使平面BCE⊥平面ABED,F为BE的中点.图2所示.
(1)求证:AE⊥平面BCE;
(2)能否在边AB上找到一点P使平面ACE与平面PCF所成角的余弦值为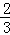 ?若存在,试确定点P的位置,若不存在请说明理由.
?若存在,试确定点P的位置,若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线l经过直线3x+4y﹣2=0与直线2x+y+2=0的交点P,且垂直于直线x﹣2y﹣1=0.求:
(Ⅰ)直线l的方程;
(Ⅱ)直线l与两坐标轴围成的三角形的面积S.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com