
| A. | 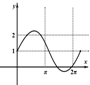 | B. |  | C. | 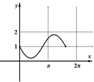 | D. |  |
分析 函数$f(x)=1+\frac{1}{a}sinax$的图象是一个正弦曲线型的图,其振幅为|$\frac{1}{a}$|,周期为|$\frac{2π}{a}$|,周期与振幅成反比,从这个方向观察四个图象,即可得出结论
解答 解:对于振幅小于2时,三角函数的周期为:T=|$\frac{2π}{a}$|,∵|$\frac{1}{a}$|<1,∴T<2π,故C,D符合,B不符合要求;
对于振幅大于2时,三角函数的周期为:T=|$\frac{2π}{a}$|,∵|$\frac{1}{a}$|>1,∴T>2π,可知A符合要求;
故选:B.
点评 由于函数的解析式中只含有一个参数,这个参数影响振幅和周期,故振幅与周期相互制约,这是本题的关键.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
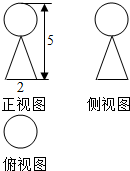
| A. | $\frac{7}{3}$π | B. | $\frac{8}{3}$π | C. | $\frac{13}{3}$π | D. | $\frac{16}{3}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com